Tam giác \({\rm{ABC}}\) vuông tại \({\rm{A}}\) có \({\rm{AB}} = 6\;{\rm{cm}},{\rm{AC}} = 8\;{\rm{cm}}\). Lấy

Câu hỏi số 656570:

Vận dụng

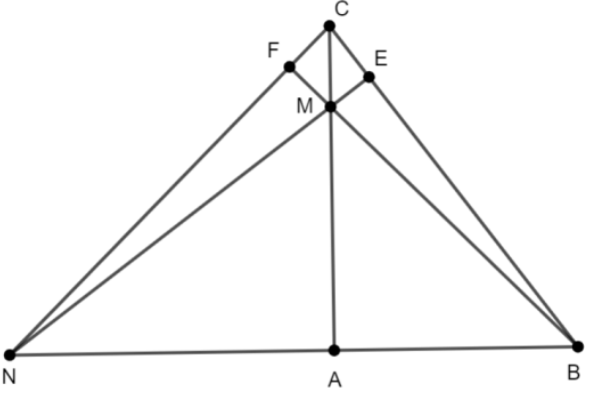
Tam giác \({\rm{ABC}}\) vuông tại \({\rm{A}}\) có \({\rm{AB}} = 6\;{\rm{cm}},{\rm{AC}} = 8\;{\rm{cm}}\). Lấy điểm \({\rm{M}}\) trên cạnh \({\rm{AC}}\) sao cho \({\rm{AM}}\) \( = {\rm{AB}}\). Kẻ ME vuông góc với \({\rm{BC}}\) tại \({\rm{E}}\).

a) Chứng minh CM.CA = CE.CB

b) Tia \({\rm{BA}}\) và tia \({\rm{EM}}\) cắt nhau tại \({\rm{N}}\), đường thẳng \({\rm{BM}}\) cắt \({\rm{NC}}\) tại \({\rm{F}}\). Chứng minh tam giác \({\rm{AMB}}\) đồng dạng với tam giác \({\rm{FMC}}\) và tam giác \({\rm{ANC}}\) vuông cân.

c) Tính tỉ số diện tích 2 tam giác \({\rm{BFN}}\) và \({\rm{MFC}}\)

Quảng cáo

Xem lời giải

Câu hỏi:656570

Phương pháp giải

a) Chứng minh \(\Delta {\rm{CEM}}\backsim\Delta {\rm{CAB}}({\rm{g}}{\rm{.g}}) \Rightarrow \dfrac{{{\rm{CM}}}}{{{\rm{CB}}}} = \dfrac{{{\rm{CE}}}}{{{\rm{CA}}}}\)(cạnh tương ứng tỉ lệ)

Suy ra đpcm.

b) Chứng minh tam giác \({\rm{AMB}}\) đồng dạng với tam giác \({\rm{FMC}}\) theo trường hợp góc – góc.

Chứng minh tam giác \({\rm{ANC}}\)là tam giác vuông có 2 nhọn bằng \(45^\circ \)

c) Chứng minh \(\Delta {\rm{FMC}}\) và \(\Delta {\rm{FBN}}\) đồng dạng theo trường hợp góc – góc.

Suy ra \(\dfrac{{{{\rm{S}}_{{\rm{BFN}}}}}}{{{{\rm{S}}_{{\rm{MFC}}}}}} = {\left( {\dfrac{{{\rm{FB}}}}{{{\rm{FM}}}}} \right)^2}\)

Giải chi tiết

a) Xét \(\Delta {\rm{CEM}}\) và \(\Delta {\rm{CAB}}\) có:

\(\angle {\rm{ACB}}\) chung; \(\angle {\rm{CEM}} = \angle {\rm{CAB}} = {90^\circ }\)

\( \Rightarrow \Delta {\rm{CEM}}\backsim\Delta {\rm{CAB}}({\rm{g}}{\rm{.g}}) \Rightarrow \dfrac{{{\rm{CM}}}}{{{\rm{CB}}}} = \dfrac{{{\rm{CE}}}}{{{\rm{CA}}}}\) (cạnh tương ứng tỉ lệ)

\( \Rightarrow CM.CA = CE.CB\) (đpcm)

b) Xét \(\Delta {\rm{CNB}}\) có: \({\rm{CA}} \bot {\rm{NB}}\); \({\rm{NE}} \bot {\rm{CB}}\)

\( \Rightarrow {\rm{M}}\) là trực tâm \(\Delta {\rm{CNB}} \Rightarrow {\rm{BF}} \bot {\rm{NC}}\)

Xét \(\Delta {\rm{FMC}}\) và \(\Delta {\rm{AMB}}\) có:

\({\rm{CFM}} = {\rm{BAM}} = {90^\circ };{\rm{CMF}} = {\rm{AMB}}\) (đối đỉnh)

\( \Rightarrow \Delta {\rm{FMC}}\backsim\Delta {\rm{AMB}}({\rm{g - g}}) \Rightarrow \angle FCM = \angle ABM\) (2 góc tương ứng)

Mà có: \({\rm{AM}} = {\rm{AB}}({\rm{gt}}) \Rightarrow \Delta {\rm{AMB}}\) vuông cân tại A

\( \Rightarrow \angle {\rm{ABM}} = {45^\circ } \Rightarrow \angle {\rm{FCM}} = {45^\circ }\)

Xét \(\Delta {\rm{ANC}}\) vuông tại \({\rm{A}}\) có: \({\rm{FCM}} = {45^\circ } \Rightarrow {\rm{ANC}} = {45^\circ }\)

\( \Rightarrow \Delta {\rm{ANC}}\) vuông cân tại A

c) Có: \({\rm{MC}} = {\rm{AC}} - {\rm{AM}} = {\rm{AC}} - {\rm{AB}} = 8 - 6 = 2(\;{\rm{cm}})\)

Xét \(\Delta {\rm{AMB}}\) vuông tại \({\rm{A}}\) có:

\({\rm{A}}{{\rm{M}}^2} + {\rm{A}}{{\rm{B}}^2} = {\rm{M}}{{\rm{B}}^2}\) (ĐL Pythagore) \( \Rightarrow MB = 6\sqrt 2 (\;{\rm{cm}})\)

Ta có: \(\Delta {\rm{FMC}}\backsim\Delta {\rm{AMB}}({\rm{cmt}}) \Rightarrow \dfrac{{{\rm{MC}}}}{{{\rm{MB}}}} = \dfrac{{{\rm{FM}}}}{{{\rm{AM}}}}\) (cặp cạnh t/ứ tỉ lệ)

\( \Leftrightarrow \dfrac{2}{{6\sqrt 2 }} = \dfrac{{{\rm{FM}}}}{6} \Leftrightarrow {\rm{FM}} = \sqrt 2 \)

Có: \(FB = BM + MF = 6\sqrt 2 + \sqrt 2 = 7\sqrt 2 \)

Xét \(\Delta {\rm{FMC}}\) và \(\Delta {\rm{FBN}}\) có:

\(\angle {\rm{CFM}} = \angle {\rm{NFB}} = {90^\circ };\angle {\rm{FCM}} = \angle {\rm{FBN}} = {45^\circ } \Rightarrow \Delta {\rm{FMC}}\backsim\Delta {\rm{FBN}}({\rm{g}}.{\rm{g}})\)

\( \Rightarrow \dfrac{{{{\rm{S}}_{{\rm{BFN}}}}}}{{{{\rm{S}}_{{\rm{MFC}}}}}} = {\left( {\dfrac{{{\rm{FB}}}}{{{\rm{FM}}}}} \right)^2} = {\left( {\dfrac{{7\sqrt 2 }}{{\sqrt 2 }}} \right)^2} = 49\)

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link