Hai bản phẳng nhiễm điện trái dấu có kích thước lớn và bằng nhau, đặt song song với nhau,

Câu hỏi số 659599:

Vận dụng cao

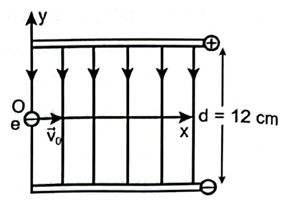
Hai bản phẳng nhiễm điện trái dấu có kích thước lớn và bằng nhau, đặt song song với nhau, cách nhau một khoảng d = 12 cm. Hiệu điện thế giữa hai bản phẳng là 24 V (hình vẽ). Một electron bay vào chính giữa hai bản phẳng theo phương vuông góc với các đường sức điện trường với vận tốc 20000 m/s. Chọn gốc tọa độ đúng tại điểm electron bắt đầu bay vào điện trường đều. Bỏ qua điện trường của Trái Đất, lực cản môi trường. Hãy tính tầm xa theo phương Ox mà electron chuyển động được. Cho khối lượng và điện tích của electron lần lượt là \(9,{1.10^{ - 31}}\,\,kg\) và \( - 1,{6.10^{ - 19}}\,\,C\).

A. 1,17 cm.

B. 1,17 mm.

C. 0,58 cm.

D. 0,58 mm.

Đáp án đúng là: B

Quảng cáo

Xem lời giải

Câu hỏi:659599

Phương pháp giải

Cường độ điện trường đều: \(E = \dfrac{U}{d}\)

Lực điện: F = qE

Gia tốc: \(a = \dfrac{F}{m}\)

Giải chi tiết

Cường độ điện trường giữa hai bản phẳng có độ lớn là:

\(E = \dfrac{U}{d}\)

Nhận xét: điện trường có chiều ngược chiều Oy nên cường độ điện trường có giá trị âm

Độ lớn lực điện tác dụng lên electron là:

\(F = \left| q \right|E = \left| q \right|\dfrac{U}{d}\)

Theo phương Ox, electron chuyển động đều với tốc độ:

\({v_x} = {v_0}\)

Phương trình chuyển động của electron theo phương Ox là:

\(x = {v_0}t \Rightarrow t = \dfrac{x}{{{v_0}}}\)

Theo phương Oy, electron chuyển động nhanh dần đều theo chiều dương với gia tốc:

\(a = \dfrac{F}{m} = \dfrac{{\left| q \right|U}}{{md}}\)

Phương trình chuyển động của electron theo phương Oy là:

\(\begin{array}{l}y = \dfrac{1}{2}a{t^2} = \dfrac{1}{2}\dfrac{{\left| q \right|U}}{{md}}{t^2}\\ \Rightarrow y = \dfrac{1}{2}\dfrac{{\left| q \right|U}}{{md}}.{\left( {\dfrac{x}{{{v_0}}}} \right)^2} = \dfrac{1}{2}\dfrac{{\left| q \right|U}}{{md{v_0}^2}}.{x^2}\end{array}\)

Tầm xa của electron đạt được khi:

\(\begin{array}{l}y = \dfrac{d}{2} \Rightarrow \dfrac{1}{2}\dfrac{{\left| q \right|U}}{{md{v_0}^2}}{x_{\max }}^2 = \dfrac{d}{2}\\ \Rightarrow {x_{\max }} = d{v_0}\sqrt {\dfrac{m}{{\left| q \right|U}}} \\ \Rightarrow {x_{\max }} = 0,12.20000.\sqrt {\dfrac{{9,{{1.10}^{ - 31}}}}{{\left| { - 1,{{6.10}^{ - 19}}} \right|.24}}} \\ \Rightarrow {x_{\max }} \approx 1,{17.10^{ - 3}}\,\,\left( m \right) = 1,17\,\,\left( {mm} \right)\end{array}\)

Đáp án cần chọn là: B

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.