Một chiếc đồng hồ cát gồm hai phần đối xứng nhau qua mặt nằm ngang và đặt trong
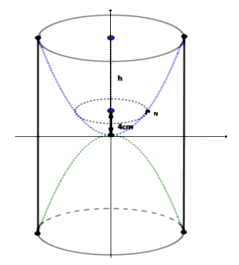
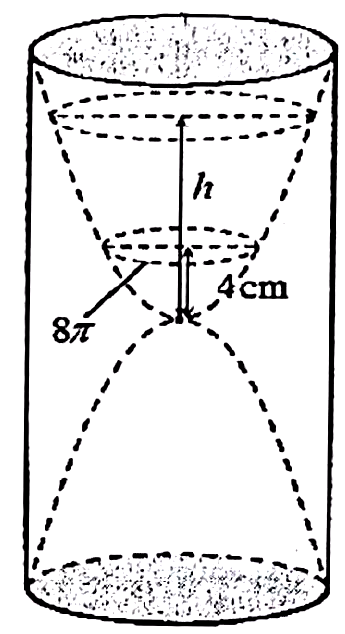
Một chiếc đồng hồ cát gồm hai phần đối xứng nhau qua mặt nằm ngang và đặt trong một hinh trụ như hình vẽ (mặt nằm ngang là mặt phằng đi qua tâm mặt cầu ngoại tiếp hình trụ và song song với hai mặt đáy của hình trư). Thiết diện thằng đứng qua trục của nó là hai parabol chung đỉnh và đối xứng nhau qua mặt nằm ngang. Ban đầu lượng cát đồn hềt ở phần trên của đồng hồ thì chiê̂u cao \(h\) của mực cát bằng \(\dfrac{3}{4}\) chiều cao của phần trên đó. Cát chảy từ trên xuống dưới với lưu lượng không đồi \(2,90\left( {{\rm{\;c}}{{\rm{m}}^3}/} \right.\) phút \()\). Khi chiều cao của cát còn \(4{\rm{\;cm}}\) thì bề mặt trên cùng của cát tạo thành một đường tròn chu vi \(8\pi \left( {{\rm{cm}}} \right)\). Biết sau 30 phút thi cát chảy hết xuống phần bên đưới của đồng hồ. Hỏi chiều cao của khối tṛ̣ bên ngoài gần với số nào nhất?
Đáp án đúng là: D
Quảng cáo
Gắn hệ trục toạ độ Oxy. Xác định toạ độ các điểm và các hàm số từ đó tính thể tích bằng tích phân
Thể tích của cát trong đồng hồ là: $V=30.2,90=87\left(\mathrm{~cm}^3\right)$.
Chọn gốc tọa độ như hình vẽ:
Chu vi của đường tròn là $8 \pi(\mathrm{~cm})$ nên bán kính đường tròn là $r=4$ khi đó điểm $N(4 ; 4)$
Gọi Parabol phía trên Ox có phương trình là: $y=a x^2$ vì parabol di qua $N(4 ; 4)$ nên ta có phương trình: $4=a \cdot 4^2 \Leftrightarrow a=\dfrac{1}{4}$ nên phương trìnhParabol có dạng: $y=\dfrac{1}{4} x^2$
Thể tích của khối cát trong đồng hồ được tính theo công thức là :
$V=\pi \int_0^h(2 \sqrt{y})^2 d y \Leftrightarrow 87=\left.2 \pi y^2\right|_0 ^h \Leftrightarrow 87=2 \pi h^2 \Leftrightarrow h \approx 3,7$
Ban đầu lượng cát dồn hết ở phần trên của đồng hồ cát thì chiều cao h của mực cát bằng $\frac{3}{4}$ chiều cao của phần trên đó nên chiều cao của khối trụ là: $3,7 \cdot \dfrac{4}{3} \cdot 2 \approx 9.87$.
Đáp án cần chọn là: D
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
