Hai thành phố \(A\) và \(B\) cách nhau một con sông. Người ta xây dựng một
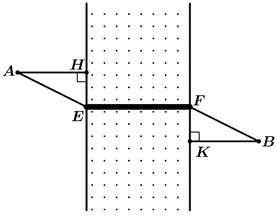
Hai thành phố \(A\) và \(B\) cách nhau một con sông. Người ta xây dựng một cây cầu \(EF\) bắc qua sông biết rằng thành phố \(A\) cách con sông một khoảng là \(4\)km và thành phố \(B\) cách con sông một khoảng là \(6\)km (hình vẽ), biết \(HE + KF = 20\)km và độ dài \(EF\) không đổi. Hỏi xây cây cầu cách thành phố \(A\) là bao nhiêu kilomet để đường đi từ thành phố A đến thành phố B là ngắn nhất (đi theo đường \(AEFB\))? Kết quả làm tròn đến phần trăm.
Đáp án đúng là:
Quảng cáo
Gọi khoảng cách từ chân cầu đến thành phố A là \(HE = x\) (km).
Vì EF không đổi nên AB ngắn nhất khi \(AE + BF\) nhỏ nhất.
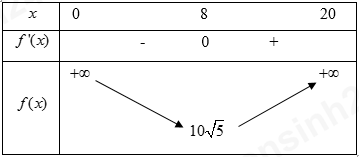
Khảo sát hàm số theo \(x\), tìm giá trị nhỏ nhất của \(AE + BF\)
Đặt \(HE = {x_{}}{,_{}}FK = y\), với \(x,\,y > 0\)
Ta có: \(HE + KF = 20 \Rightarrow x + y = 20\), \(\left\{ \begin{array}{l}AE = \sqrt {16 + {x^2}} \\BF = \sqrt {36 + {y^2}} = \sqrt {36 + {{\left( {20 - x} \right)}^2}} \end{array} \right.\)
Nhận xét: Vì \(EF\) không đổi nên \(AB\) ngắn nhất khi \(AE + BF\) nhỏ nhất.
Ta có \(AE + BF\)\( = \sqrt {{x^2} + 16} + \sqrt {{{\left( {20 - x} \right)}^2} + 36} = \sqrt {{x^2} + 16} + \sqrt {{x^2} - 40x + 436} = f\left( x \right)\)
Đạo hàm \(f'\left( x \right) = \dfrac{x}{{\sqrt {{x^2} + 16} }} + \dfrac{{x - 20}}{{\sqrt {{x^2} - 40x + 436} }} = 0 \Rightarrow x = 8,\,\forall x \in \left( {0;20} \right)\)\(\)
Bảng biến thiên
Vậy \(AE = \sqrt {{8^2} + 16} \approx 8,94\) km
Đáp án cần điền là: 8,94
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
