Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc cuối HK1 lớp 10, 11, 12 tất cả các môn - Trạm số 1 - Ngày 20-21/12/2025 Xem chi tiết
Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn toán

Các thiên thạch có đường kính lớn hơn 140m và có thể lại gần

Câu hỏi số 738345:
Vận dụng

Các thiên thạch có đường kính lớn hơn 140m và có thể lại gần Trái Đất ở khoảng cách nhỏ hơn 7.500.000km được coi là những vật thể có khả năng va chạm gây nguy hiểm cho Trái Đất. Để theo đõi những thiên thạch này, các nhà nghiên cứu của trung tâm Vũ Trụ Nasa đã thiết lập các trạm quan sát các vật thể bay gần Trái Đất. Giả sử có một hệ thống quan sát có khả năng theo dõi các vật thể ở độ cao không vượt quá 4600 km so với mực nước biển. Coi Trái Đất là khối cầu có bán kính 6400 km. Chọn hệ trục tọa độ Oxyz trong không gian có gốc O tại tâm Trái Đất và đơn vị độ dài trên mỗi trục tọa độ là 1000 km. Một thiên thạch (coi như một hạt) chuyển động với tốc độ \({v_1} = 2\sqrt 2  \cdot {10^3}(\;{\rm{km}}/{\rm{h}})\) không đổi theo đường thẳng xuất phát từ điểm \(M(0;5;12)\) đến \(N(12;5;0)\)

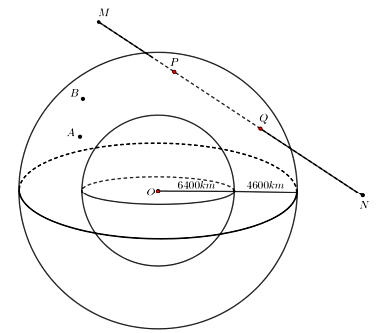
Đúng Sai
a) Khoảng cách thiên thạch gần với trái đất nhất có độ dài bằng 3449 km (làm tròn đến hàng đơn vị)
b) Các nhà nghiên cứu của trung tâm vũ trụ Nasa đưa ra giả thiết nếu lúc thiên thạch đang ở vị trí M bất ngờ đổi hướng và lao xuống trái đất với phương thẳng thì quãng đường dài nhất nó có thể va chạm với trái đất là 14490 km (làm tròn đến hàng đơn vị).
c) Tại thời điểm thiên thạch đang ở vị trí M thì có 2 vệ tinh đang ở vị trí \(A( - 6; - 5; - 6)\), \(B(7; - 6;7)\) có vận tốc khác nhau di chuyển trong mặt phẳng trung trực của MN và luôn cách trái đất với khoảng cố định. Khoảng cách xa nhất của 2 vệ tinh có thể đạt là 18412 km (làm tròn đến hàng đơn vị).
d) Nếu vệ tinh A đi với vận tốc \({v_2} = \dfrac{{\pi \sqrt {97} }}{3}{.10^3}\) km/h thì sẽ va chạm với thiên thạch.

Đáp án đúng là: Đ; S; S; Đ

Quảng cáo

Xem lời giải
Câu hỏi:738345
Phương pháp giải

a) Viết phương trình MN. Tìm toạ độ H là hình chiếu của O xuống MN.

Khi đó khoảng cách ngắn nhất bằng OH.

b) Gọi M’ là điểm va chạm của M với Trái Đất

\( \Rightarrow MM'\) lớn nhất khi MM' là tiếp tuyến kẻ từ M tới mặt cầu – là bề mặt trái đất

c) Vậy AB lớn nhất khi O, A, B thẳng hàng.

d) Để vệ tinh va chạm với thiên thạch thì chỉ có thể va chạm tại I là trung điểm của MN

Giải chi tiết

a) Đúng.

\(M(0;5;12)\), \(N(12;5;0)\) nên \(\overrightarrow {MN} \left( {12,0, - 12} \right)\)

Chọn MN có VTCP là \(\overrightarrow u  = \left( {1,0, - 1} \right)\), qua \(M(0;5;12)\) có phương trình \(\left\{ \begin{array}{l}x = t\\y = 5\\z = 12 - t\end{array} \right.\)

Gọi \(OH \bot MN\) tại H. Khi đó \(H\left( {t,5,12 - t} \right)\)

\(\begin{array}{l} \Rightarrow \overrightarrow {OH} \left( {t,5,12 - t} \right) \bot \overrightarrow u \left( {1,0, - 1} \right)\\ \Rightarrow t.1 + 5.0 + \left( {12 - t} \right).\left( { - 1} \right) = 0\\ \Leftrightarrow t = 6 \Rightarrow H\left( {6,5,6} \right)\end{array}\)

\( \Rightarrow OH = \sqrt {{6^2} + {5^2} + {6^2}}  = \sqrt {97} \)

Suy ra khoảng cách ngắn nhất từ tâm trái đất đến MN là \(\sqrt {97} .1000 \approx 9849\) km.

Khoảng cách thiên thạch gần với trái đất nhất có độ dài bằng 9849 – 6400 = 3449 km.

b) Sai.

Gọi M’ là điểm va chạm của M với Trái Đất

\( \Rightarrow MM'\) lớn nhất khi \(MM'\) là tiếp tuyến kẻ từ M tới mặt cầu – là bề mặt trái đất

\( \Rightarrow MM' = \sqrt {O{M^2} - O{{M'}^2}}  = \sqrt {{{13}^2} - 6,{4^2}} \)

Hay quãng đường dài nhất là \(\sqrt {{{13}^2} - 6,{4^2}} .1000 \approx 11316\) km.

c) Sai

 \(A( - 6; - 5; - 6)\), \(B(7; - 6;7) \Rightarrow OA = \sqrt {97} ,OB = \sqrt {134} \)

\(AB \le OA + OB = \sqrt {97}  + \sqrt {134}  \approx 21,4247\)

Vậy AB lớn nhất bằng 21425km khi O, A, B thẳng hàng.

d) Đúng.

\(M(0;5;12)\), \(N(12;5;0)\) nên trung điểm I của MN có tọa độ \(I\left( {6,5,6} \right)\)

Do \(OA = \sqrt {97} \) không đổi nên A luôn thuộc mặt cầu có tâm O, bán kính \(OA = \sqrt {97} \)

Để vệ tinh va chạm với thiên thạch thì chỉ có thể va chạm tại I

Khi đó \(AI = \dfrac{{MN}}{2} = \dfrac{{12\sqrt 2 }}{2} = 6\sqrt 2 \)

Thời gian để thiên thạch di chuyển từ M đến I là \({t_1} = \dfrac{{6\sqrt 2 {{.10}^3}}}{{2\sqrt 2 {{.10}^3}}} = 3\) (giờ)

Nhận thấy A, I đối xứng nhau qua O nên quãng đường để vệ tinh di chuyển từ A đến I là một đường cong có độ dài bằng nửa chu vi đường tròn bán kính OA và bằng \(\pi .OA = \sqrt {97} \pi \)

Vậy thời gian để vệ tinh đi từ A đến I là \({t_2} = \dfrac{{\sqrt {97} \pi {{.10}^3}}}{{\dfrac{{\pi \sqrt {97} }}{3}{{.10}^3}}} = 3\) (giờ)

Vậy vệ tinh và thiên thạch có va chạm.

Đáp án cần chọn là: Đ; S; S; Đ

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn