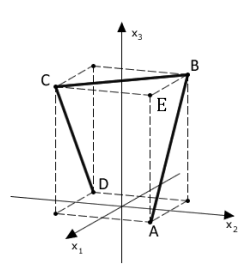
Hình 1 minh họa Saarpolygon, một đài tưởng niệm bên trong nhớ về hoạt động khai
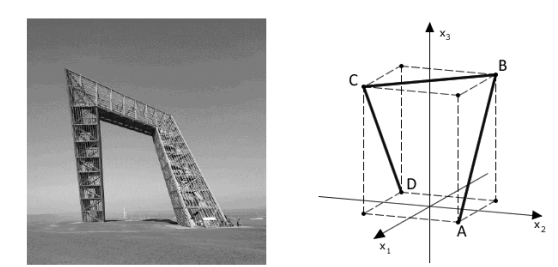
Hình 1 minh họa Saarpolygon, một đài tưởng niệm bên trong nhớ về hoạt động khai thác than đã ngừng tại Saarland. Saarpolygon được mô phỏng trong hệ tọa độ bằng đường gấp khúc bao gồm ba đoạn thẳng AB, BC và CD với các điểm \(A\left( {11,11,0} \right),B\left( { - 11,11,28} \right),C\left( {11, - 11,28} \right),\)và \(D\left( { - 11, - 11,0} \right)\) (xem Hình vẽ). A, B, C và D là các đỉnh điểm của một hình hộp chữ nhật. Mỗi đơn vị dài trong hệ tọa độ tương đương với một mét trong thực tế. Xét tính đúng sai của các khẳng định sau:
| Đúng | Sai | |
|---|---|---|
| a) B, C đối xứng nhau qua trục Oz | ||
| b) Độ dài của đường gấp khúc trong thực tế nhỏ hơn 100m | ||
| c) Mặt phẳng (P) chứa các điểm A, B và C; mặt phẳng (Q) chứa các điểm B, C và D. Góc giữa hai mặt phẳng (P) và (Q) là \({76^0}\) (làm tròn đến hàng đơn vị). | ||
| d) Mặt phẳng (P) chia hình hộp thành 2 phần có thể tích là \({V_1} < {V_2}\). Khi đó \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{1}{6}\) |
Đáp án đúng là: Đ; S; S; S
Quảng cáo
a) Hai điểm đối xứng nhau qua trục Oz nếu hoành độ, tung độ đối nhau, cao độ bằng nhau
b) Tính độ dài AB + BC + CD và so sánh 100
c) Góc giữa hai mặt phẳng là góc giữa hai vecto pháp tuyến của hai mặt phẳng đó.
d) Tính thể tích \(\dfrac{{{V_1}}}{V}\) từ đó suy ra \(\dfrac{{{V_1}}}{{{V_2}}}\).
a) Đúng. \(B\left( { - 11,11,28} \right),C\left( {11, - 11,28} \right)\) có \({x_B} = - {x_C},{y_B} = - {y_C},{z_B} = {z_C}\) nên B, C đối xứng nhau qua Oz
b) Sai. Ta có \(A\left( {11,11,0} \right),B\left( { - 11,11,28} \right),C\left( {11, - 11,28} \right),\)\(D\left( { - 11, - 11,0} \right)\) nên:
\(\begin{array}{l}\overrightarrow {AB} = \left( { - 22,0,28} \right) \Rightarrow AB = 2\sqrt {317} \\\overrightarrow {BC} = \left( {22, - 22,0} \right) \Rightarrow BC = 22\sqrt 2 \\\overrightarrow {CD} = \left( { - 22,0, - 28} \right) \Rightarrow CD = 2\sqrt {317} \\ \Rightarrow AB + BC + CD = 4\sqrt {317} + 22\sqrt 2 \approx 102m\end{array}\)
c) Đúng. Ta có \(A\left( {11,11,0} \right),B\left( { - 11,11,28} \right),C\left( {11, - 11,28} \right),\)\(D\left( { - 11, - 11,0} \right)\)
(P) qua A, B, C nên \(\overrightarrow {{n_{\left( P \right)}}} = \left[ {\overrightarrow {AB} ,\overrightarrow {BC} } \right] = \left( {22.28,22.28,{{22}^2}} \right)\) nên chọn \(\overrightarrow {{n_1}} \left( {14,14,11} \right)\)
(Q) qua B, C, D nên \(\overrightarrow {{n_{\left( Q \right)}}} = \left[ {\overrightarrow {BC} ,\overrightarrow {CD} } \right] = \left( {22.28; 22.28; - {{22}^2}} \right)\) nên chọn \(\overrightarrow {{n_2}} \left( {14, 14, - 11} \right)\)
Khi đó góc giữa (P) và (Q) là góc giữa 2 vecto pháp tuyến của hai mặt phẳng
Ta có \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \dfrac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \dfrac{{{{14^2+14^2-11}^2}}}{{{{\left( {\sqrt {{{14}^2} + {{14}^2} + {{11}^2}} } \right)}^2}}} = \dfrac{{271}}{{513}}\)
\( \Rightarrow \left( {\left( P \right),\left( Q \right)} \right) \approx {58^0}\)
d) Sai. Ta có (P) chia hình hộp thành 2 phần là ABEC và phần còn lại.
Ta có \({V_1} = {V_{ABEC}} = \dfrac{1}{3}AE.{S_{BEC}} = \dfrac{1}{3}.28.\dfrac{1}{2}.22.22 = \dfrac{{6776}}{3}\)
\(V = 22.22.28 = 13552\)
\( \Rightarrow \dfrac{{{V_1}}}{V} = \dfrac{1}{6} \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{1}{5}\)
Đáp án cần chọn là: Đ; S; S; S
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
