Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc cuối HK1 lớp 10, 11, 12 tất cả các môn - Trạm số 1 - Ngày 20-21/12/2025 Xem chi tiết
Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn toán

Nhà máy địa nhiệt sử dụng nhiệt từ lòng đất để tạo ra điện hoặc cung

Câu hỏi số 748702:
Vận dụng

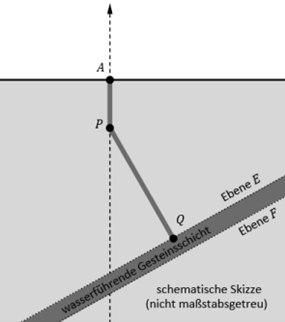
Nhà máy địa nhiệt sử dụng nhiệt từ lòng đất để tạo ra điện hoặc cung cấp năng lượng cho các mục đích sưởi ấm. Một nhà máy địa nhiệt bơm nước nóng từ một lớp đá chứa nước lên mặt đất thông qua một hệ thống ống dẫn. Hệ thống này được mô hình với mặt phẳng \(Oxy\) của hệ trục tọa độ tương ứng với bề mặt Trái Đất, mỗi đơn vị độ dài trong hệ tọa độ tương ứng với một 1000m trong thực tế. Ống dẫn nước bao gồm hai đoạn, được mô hình hóa bởi các đoạn thẳng \(AP\) và \(PQ\) với các điểm \(A(0;0; 0)\), \(P(0;0;-1)\) và \(Q\left(1 ; 1 ; \dfrac{-7}{2}\right)\).

Đúng Sai
a)

Tổng chiều dài của ống dẫn nước là khoảng 3872m.
b) Tại điểm giao giữa hai đoạn AP và PQ, hướng của ống dẫn bị lệch đi một góc \({30^o}\).
c) Trong mô hình, mặt phẳng \((E)\) là bề mặt trên của lớp đá chứa nước và mặt phẳng \((F)\) (song song với \((E)\)) là bề mặt dưới của lớp đá. Đoạn thẳng \(PQ\) vuông góc với mặt phẳng \((E)\) tại \(Q\). Phương trình mặt phẳng \((E)\) là: \(4x + 4y – 10z - 43 = 0\).
d) Nếu hệ thống ống dẫn được kéo dài thẳng và xuyên qua lớp đá chứa nước ở độ sâu 3600m so với mặt đất. Khi đó, độ dày của lớp đá chứa nước là 100m.

Đáp án đúng là: Đ; S; Đ; S

Quảng cáo

Xem lời giải
Câu hỏi:748702
Phương pháp giải

a) Tính độ dài \(AP+PQ\).

b) Công thức tính góc giữa hai vectơ: \(\cos (\overrightarrow{A P}, \overrightarrow{P Q})=\dfrac{\overrightarrow{A P} \cdot \overrightarrow{P Q}}{|\overrightarrow{A P}| \cdot|\overrightarrow{P Q}|}\)

c) Viết phương trình mặt phẳng \((E)\) đi qua điểm \(Q\left(1 ; 1 ; \dfrac{-7}{2}\right)\) và nhận vectơ \(\vec{n}=4 \cdot \overrightarrow{P Q}\) làm vectơ pháp tuyến.

d) Viết phương trình đường thẳng \(PQ\), xác định toạ độ điểm \(R \in PQ\).

Tính độ dài \(QR\).

Giải chi tiết

a) Đúng: Có \(A(0;0; 0)\), \(P(0;0;-1)\) và \(Q(1;1;-3,5)\).

\(\overrightarrow{A P}(0 ; 0 ;-1) \Rightarrow A P=1\) và \(\overrightarrow{P Q}\left(1 ; 1 ; \dfrac{-5}{2}\right) \Rightarrow P Q=\dfrac{\sqrt{33}}{2}\)

Ta có \(A P+P Q=1+\dfrac{\sqrt{33}}{2} \approx 3,872\).

Chiều dài hệ thống ống dẫn nước là khoảng 3872m.

b) Sai: Có \(\overrightarrow{A P}(0 ; 0 ;-1), \overrightarrow{P Q}\left(1 ; 1 ; \dfrac{-5}{2}\right)\)

\(\cos (\overrightarrow{A P}, \overrightarrow{P Q})=\dfrac{\overrightarrow{A P} \cdot \overrightarrow{P Q}}{|\overrightarrow{A P}| \cdot|\overrightarrow{P Q}|}=\dfrac{\dfrac{5}{2}}{1 \cdot \dfrac{\sqrt{33}}{2}}=\dfrac{5 \sqrt{33}}{33} \)

\(\Rightarrow(\overrightarrow{A P}, \overrightarrow{P Q}) \approx 29,5^{\circ}.\)

c) Đúng: Mặt phẳng \((E)\) đi qua điểm \(Q\left(1 ; 1 ; \dfrac{-7}{2}\right)\) và nhận vectơ \(\vec{n}=4 \cdot \overrightarrow{P Q}\left(1 ; 1 ; \dfrac{-5}{2}\right)=(4 ; 4 ;-10)\) làm vectơ pháp tuyến.

Phương trình mặt phẳng \((E)\) có dạng: : \(4 x+4 y-10 z+d=0\)

Thay tọa độ điểm \(Q\left(1 ; 1 ; \dfrac{-7}{2}\right)\) vào phương trình, ta được phương trình mặt phẳng \((E): 4 x+4 y-10 z-43=0\).

d) Sai: Ta có phương trình đường thẳng \(P Q:\left\{\begin{array}{l}x=t \\ y=t \\ z=-1-\dfrac{5}{2} t\end{array}\right.\)

Gọi \(R\left(t ; t ;-1-\dfrac{5}{2} t\right) \in P Q\) là giao điểm của đường thẳng \(PQ\) với mặt phẳng \((F)\).

Vì ở độ sâu 3600m nên \(z_R=-1-\dfrac{5}{2} t=-3,6 \Rightarrow t=1,04\).

Suy ra \(R(1,04 ; 1,04 ; 3,6)\), có \(Q(1 ; 1 ;-3,5)\).

\(Q R=\sqrt{(0,04)^2+(0,04)^2+(-3,6+3,5)^2}=\sqrt{0,0132}\)

Độ dày của lớp đá chứa nước là \(\sqrt{0,0132} \cdot 1000 \approx 115 m\).

Đáp án cần chọn là: Đ; S; Đ; S

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn