Trong một cuộc thử tên lửa, Triều Tiên đã cho phóng một quả tên lửa
Trong một cuộc thử tên lửa, Triều Tiên đã cho phóng một quả tên lửa có gắn đầu đạn hạt nhân với vận tốc \(v\left( t \right) = \dfrac{1}{{90000000}}{t^3} + \dfrac{1}{{500}}t + 1\,\,\left( {m/s} \right)\) trong đó \(t\) đơn vị giây tính từ lúc tên lửa Triều Tiên bắt đầu phóng và dự tính sẽ rơi xuống một vùng biển. Đi được 1 giờ thì bay ngang vùng biển thuộc chủ quyền của Nhật Bản nay lập tức Rada nhận được tín hiệu về căn cứ quân đội. Khi nhận được tín hiệu và gửi tín hiệu về căn cứ quân đội. Khi nhận được tín hiệu của Rada sau 30 phút quân đội Nhật Bản đã cho phóng 1 quả tên lửa tầm trung đã xác định sẵn mục tiêu đi với gia tốc \(a\left( {{t_1}} \right) = \dfrac{1}{{4500}}{t_1} + \dfrac{n}{{100}}\,\,\left( {m/{s^2}} \right),\,\,n > 0\) trong đó \({t_1}\) đơn vị giây tính từ lúc tên lửa tầm trung bắt đầu phóng.
| Đúng | Sai | |
|---|---|---|
| a) Vận tốc của tên lửa tầm trung được biểu thị dưới hàm \(v\left( {{t_1}} \right) = \dfrac{1}{{9000}}t_1^2 + \dfrac{n}{{100}}{t_1}\,\,\left( {m/s} \right),\,\,n > 0\) | ||
| b) Kể từ khi bị Rada phát hiện đến lúc Nhật Bản phóng tên lửa thì quả tên lửa gắn đầu đạn hạt nhân đi được \(1913,4km\). | ||
| c) Sau 15 phút phóng tên lửa tầm trung hạ được mục tiêu biết quảng đường nó đi được bằng \(\dfrac{1}{2}\) quãng đường tên lửa Triều Tiên đi được trong 15 phút đó khi đó giá trị \(n > 100\) | ||
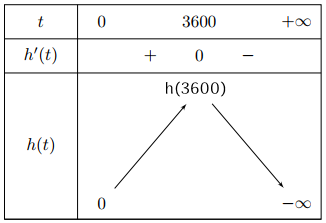
| d) Giả sử hàm \(h\left( t \right) = \dfrac{{ - 5m}}{{648}}{t^2} + \dfrac{{500m}}{9}t + a\,\,\left( {m > 0,\,\,a \in \mathbb{R}} \right)\) (đơn vị: mét) thể hiện độ cao của quả tên lửa gắn đầu đạn hạt nhân so với mực nước biển. Khi quả tên lửa của Triều Tiên đạt độ cao lớn nhất thì quãng đường nó đi được là \(483,12km\) |
Đáp án đúng là: Đ; Đ; Đ; Đ
Quảng cáo
a) \(v\left( {{t_1}} \right) = \int {a\left( {{t_1}} \right)d{t_1}} \)
b) Tìm \(s\left( t \right) = \int {v\left( t \right)dt} \) từ đó tính \(s\left( {5400} \right) - s\left( {3600} \right)\)
c) Tính quãng đường sau 15 phút thì tên lửa của Triều Tiên và Nhật Bản đi được sau đó giải phương trình \({S_{NB}} = \dfrac{1}{2}{S_{TT}}\) tìm n và kết luận.
d) Khi \(t = 0\) thì \(h\left( 0 \right) = 0 \Leftrightarrow a = 0\) từ đó tìm \(h\left( t \right)\) và tìm độ cao lớn nhất.
a) Vận tốc của tên lửa tầm trung được biểu thị dưới hàm
\(v\left( {{t_1}} \right) = \int {a\left( {{t_1}} \right)d{t_1}} = \dfrac{1}{{9000}}t_1^2 + \dfrac{n}{{100}}{t_1} + {v_0}\,\,\left( {m/s} \right)\,\,\left( {{v_0} > 0,\,\,n > 0} \right)\)
Khi \({t_1} = 0\) thì \(v\left( 0 \right) = 0\)
Suy ra \(\dfrac{1}{{9000}}{.0^2} + \dfrac{n}{{100}}.0 + C = 0 \Leftrightarrow C = 0\)
Vậy \(v\left( {{t_1}} \right) = \dfrac{1}{{9000}}t_1^2 + \dfrac{n}{{100}}{t_1}\)
b) Thời gian từ lúc Rada nhận được tín hiệu tới lúc Nhật Bản phóng tên lửa là \(1,5\) giờ
Đổi 1,5 giờ = 5400 giây
Ta có: \(s\left( t \right) = \int {v\left( t \right)dt} = \dfrac{{{t^4}}}{{360000000}} + \dfrac{{{t^2}}}{{1000}} + t\)
Khi đó quãng đường mà tên lửa gắn đầu đạn hạt nhân đi được là
\(s\left( {5400} \right) - s\left( {3600} \right) = 1913400\left( m \right) = 1913,4\left( {km} \right)\)
c) Sau 15 phút thì tên lửa của Triều Tiên đi được là
\({S_{TT}} = \int\limits_{5400}^{6300} {v\left( t \right)dt} = \int\limits_{5400}^{6300} {\left( {\dfrac{1}{{90000000}}{t^3} + \dfrac{1}{{500}}t + 1} \right)dt} = 2025292,5\left( m \right)\)
Sau 15 phút, tên lửa của Nhật Bản đi được là
\({S_{NB}} = \int\limits_0^{900} {v\left( {{t_1}} \right)d{t_1} = \int\limits_0^{900} {\left( {\dfrac{1}{{9000}}t_1^2 + \dfrac{n}{{100}}{t_1}} \right)d{t_1}} } \)
\( = \int\limits_0^{900} {\dfrac{1}{{9000}}t_1^2d{t_1} + n\int\limits_0^{900} {\dfrac{1}{{100}}{t_1}d{t_1}} = 27000 + 4050n} \)
Theo giả thiết \({S_{NB}} = \dfrac{1}{2}{S_{TT}} \Leftrightarrow 27000 + 4050n = \dfrac{1}{2}.2025292,5 \Leftrightarrow n = 243,4\)
Vậy \(n > 100\)
d) Khi \(t = 0\) thì \(h\left( 0 \right) = 0 \Leftrightarrow a = 0\)
Suy ra \(h\left( t \right) = \dfrac{{ - 5m}}{{648}}{t^2} + \dfrac{{500m}}{9}t\)
\(h'\left( t \right) = - \dfrac{{5m}}{{648}}.2t + \dfrac{{500m}}{9} = 0 \Leftrightarrow t = 3600\)
Bảng biến thiên:
Độ cao lớn nhất của tên lửa Triều Tiên là \(h\left( {3600} \right)\,\,\left( m \right)\)
Quãng đường tên lửa Triều Tiên đi được khi đạt độ cao lớn nhất là
\(S = \dfrac{1}{{1000}}\int\limits_0^{3600} {v\left( t \right)dt} = \dfrac{1}{{1000}}\int\limits_0^{3600} {\left( {\dfrac{1}{{90000000}}{t^3} + \dfrac{1}{{500}}t + 1} \right)dt} = 483,12\,\,\left( {km} \right)\)
Đáp án: a đúng| b đúng| c đúng| d đúng.
Đáp án cần chọn là: Đ; Đ; Đ; Đ
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
