Một kiến trúc sư muốn thiết kế một khung cửa sổ hình chữ nhật lắp vào một

Câu hỏi số 758525:

Vận dụng

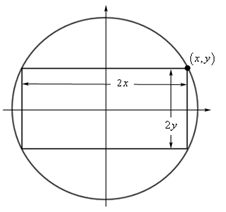
Một kiến trúc sư muốn thiết kế một khung cửa sổ hình chữ nhật lắp vào một ô tròn trên tường có bán kính 4 mét. Kiến trúc sư muốn cửa sổ có kích thước lớn nhất để đón ánh sáng vào căn phòng. Hỏi diện tích lớn nhất của cửa sổ có thể đạt được là bao nhiêu?

A. 30

B. 31

C. 32

D. 33

Đáp án đúng là: C

Quảng cáo

Xem lời giải

Câu hỏi:758525

Phương pháp giải

- Bài toán yêu cầu tìm diện tích lớn nhất của hình chữ nhật nội tiếp hình tròn có bán kính bằng 4.

- Đặt trục tọa độ với tâm đường tròn trùng với gốc tọa độ. Lập phương trình đường tròn và biểu

diễn hàm diện tích của hình chữ nhật.

- Tính đạo hàm của hàm diện tích và tìm giá trị lớn nhất của hàm số.

Giải chi tiết

Đặt trục tọa độ sao cho tâm đường tròn (tâm hình chữ nhật) trùng gốc tọa độ và điểm \((x,y)\) như hình:

Ta có phương trình đường tròn \((C):\)\({x^2} + {y^2} = 16\) hay \(y = \pm \sqrt {16 - {x^2}} .\)

Khi đó chiều dài của sổ hình chữ nhật là \(2x\), chiều rộng là \(2y\), với \(x > 0,y > 0\) nằm trên đường tròn \((C)\)

Diện tích cửa sổ hình chữ nhật là \(S = 2x.2y = 4xy = 4x\sqrt {16 - {x^2}} \)

Xét hàm số \(S(x) = 4x\sqrt {16 - {x^2}} \) với \(0 \le x \le 4\)

Có \(S'(x) = 4\sqrt {16 - {x^2}} - \dfrac{{4{x^2}}}{{\sqrt {16 - {x^2}} }} = \dfrac{{ - 8{x^2} + 64}}{{\sqrt {16 - {x^2}} }}\).

\(S'(x) = 0 \Leftrightarrow - 8{x^2} + 64 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\sqrt 2 \\x = - 2\sqrt 2 {\rm{(loai)}}\end{array} \right.\)

Ta có \(S(0) = 0\); \(S(4) = 4.4.\sqrt {16 - {4^2}} = 0;\)

\(S(2\sqrt 2 ) = 4.2\sqrt 2 .\sqrt {16 - {{\left( {2\sqrt 2 } \right)}^2}} = 32.\)

Vậy cửa sổ hình chữ nhật lớn nhất nội tiếp đường tròn có bán kính bằng 4 sẽ có hình vuông với diện tích 32, chiều dài và chiều rộng bằng \(2\sqrt 2 .\)

Đáp án cần chọn là: C

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.