Cho hình H là một tam giác đều cạnh \(a\). Người ta lần lượt thực hiện
Cho hình H là một tam giác đều cạnh \(a\). Người ta lần lượt thực hiện các bước như sau:
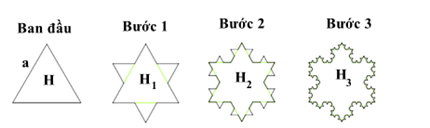
Bước 1: Chia mỗi cạnh của hình H thành ba đoạn thẳng bằng nhau. Trên mỗi đoạn thẳng ở giữa, dựng một tam giác đều nằm ngoài hình H, sau đó xóa bỏ đoạn ở giữa, ta được hình \({H_1}\) (tham khảo hình vẽ).
Bước 2: Tiếp tục lặp lại quá trình trên với mỗi cạnh của hình \({H_1}\) ta được hình \({H_2}\)
Sau nhiều bước thực hiện như trên, ta được một hình giống như bông tuyết, gọi là bông tuyết Von Koch.
| Đúng | Sai | |
|---|---|---|
| a) Độ dài mỗi cạnh của hình \({H_1}\) là \(\dfrac{a}{3}\) |
||
| b) Với mọi số tự nhiên\({\rm{\;}}n \ge 2\) thì độ dài mỗi cạnh của hình \({H_{n - 1}}\) gấp 3 lần độ dài mỗi cạnh của hình \({H_n}\). | ||
| c) Gọi \({u_1},{u_2},.....,{u_n},....\) lần lượt là số cạnh của các hình \({H_1},{H_2},....{H_n},...\). Khi đó, dãy số \({u_1},{u_2},{u_3},{u_4},....\) theo thứ tự lập thành một cấp số nhân có công bội \(q = 4\). | ||
| d) Chu vi của hình bông tuyết Von Koch \({H_{16}}\) lớn hơn 100 lần chu vi của hình H. |
Đáp án đúng là: Đ; Đ; Đ; S
Quảng cáo
Phân tích đầu bài, suy ra độ dài cạnh và số cạnh của các hình \(H_n\).
Đáp án cần chọn là: Đ; Đ; Đ; S
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
