Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc cuối HK1 lớp 10, 11, 12 tất cả các môn - Trạm số 1 - Ngày 20-21/12/2025 Xem chi tiết
Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn toán

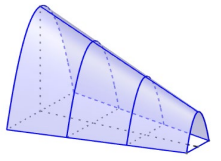
Một đường hầm mô hình như hình vẽ có chiều dài $5(~\text{cm})$. Khi

Câu hỏi số 775984:
Vận dụng

Một đường hầm mô hình như hình vẽ có chiều dài $5(~\text{cm})$. Khi cắt mô hình này bởi các mặt phẳng vuông góc với đáy của nó, ta được mặt cắt là một hình parabol có độ dài đáy gấp đôi chiều cao. Ở đó hình parabol là hình phẳng được giới hạn bởi một đường parabol và đoạn thẳng nối hai điểm thuộc parabol đồng thời vuông góc với trục đối xứng của parabol đó được gọi là đáy, khoảng cách từ đỉnh của parabol xuống đáy gọi là chiều cao. Chiều cao của mỗi mặt cắt hình parabol cho bởi công thức $y = 3 - \dfrac{2}{5}x(~\text{cm})$, với $x(~\text{cm})$ là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình đến mặt phẳng chứa mặt cắt.

Đúng Sai
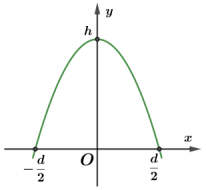
a) Nếu một hình parabol có đáy bằng $d$ và chiều cao bằng $h$ như hình vẽ thì phương trình của parabol là $y = - \dfrac{4h}{d^{2}}x^{2} + h$.
b) Diện tích cửa lớn của đường hầm mô hình bằng $12\left( {~\text{cm}^{2}} \right)$.
c) Chiều cao cửa nhỏ của đường hầm mô hình bằng $2(~\text{cm})$.
d) Nếu người ta làm một khối có kích thước như mô hình đường hầm ở trên bằng nguyên liệu có giá 5,4 triệu đồng cho mỗi $\text{cm}^{3}$ thì số tiền cần bỏ ra để mua nguyên liệu là 156 triệu đồng.

Đáp án đúng là: Đ; Đ; S; Đ

Quảng cáo

Xem lời giải
Câu hỏi:775984
Phương pháp giải

Viết phương trình parabol, ứng dụng tích phân để tính diện tích parabol và thể tích.

Giải chi tiết

a) Đúng: Giả sử parabol có dạng $y = ax^{2} + bx + c$

Vì đỉnh parabol là $I(0;h)$ nên $\left. \dfrac{- b}{2a} = 0\Rightarrow b = 0 \right.$ và $y(0) = c = h$

Parabol đi qua điểm $\left( {\dfrac{d}{2};0} \right)$, suy ra $\left. a\left( \dfrac{d}{2} \right)^{2} + h = 0\Rightarrow a = \dfrac{- 4h}{d^{2}} \right.$

Vậy phương trình của parabol là $y = - \dfrac{4h}{d^{2}}x^{2} + h$.

b) Đúng: Có chiều cao của cửa lớn là $h = 3$.

Độ dài đáy gấp đôi chiều cao, ta có $d = 6$.

Diện tích cửa lớn là $S = \dfrac{2}{3}.h.d = \dfrac{2}{3}.3.6 = 12$$(cm^{2})$.

c) Sai: Ta có đường hầm mô hình có chiều dài $5(~\text{cm})$.

Khoảng cách từ cửa lớn đến cửa nhỏ là 5

Suy ra chiều cao cửa nhỏ là $y = 3 - \dfrac{2}{5}.5 = 1(~\text{cm})$

d) Đúng: Diện tích của parabol là $\int\limits_{- \dfrac{d}{2}}^{\dfrac{d}{2}}{\left( {- \dfrac{4h}{d^{2}}x^{2} + h} \right)dx}$

Mà $d = 2h$ nên ta có $S = {\int\limits_{- h}^{h}\left( {- \dfrac{1}{h}x^{2} + h} \right)}dx = \left. \left( {\dfrac{x^{3}}{3} + hx} \right) \right|_{- h}^{h}$

Lại có $h = 3 - \dfrac{2}{5}x$, suy ra $S = \dfrac{4}{3}\left( {3 - \dfrac{2}{5}x} \right)^{2}$

Thể tích không gian bên trong đường hầm mô hình là

${\int\limits_{0}^{5}{\left( {\dfrac{4}{3}\left( {3 - \dfrac{2}{5}x} \right)^{2}} \right)dx}} = \dfrac{260}{9}(cm^{3})$

Số tiền bỏ ra để mua nguyên liệu là $\dfrac{260}{9}.5,4 = 156$ triệu đồng.

Đáp án cần chọn là: Đ; Đ; S; Đ

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn