Gia đình ông Bình xây một cái chòi hình bát giác, trong đó mái chòi $(H)$ có dạng hình "chóp bát

Câu hỏi số 775990:

Vận dụng

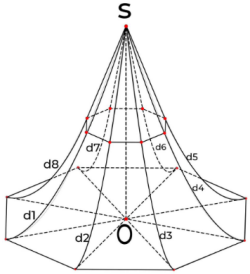
Gia đình ông Bình xây một cái chòi hình bát giác, trong đó mái chòi $(H)$ có dạng hình "chóp bát giác cong đều" có trần bằng gỗ như hình vẽ bên dưới. Đáy của $(H)$ là một hình bát giác đều có cạnh là $a = \dfrac{3\sqrt{2\sqrt{2} + 4}}{\sqrt{2} + 2}(m)$. Chiều cao $SO = 6m$ (SO vuông góc với mặt phẳng đáy). Các cạnh bên của $(H)$ là các sợi dây thép $d_{1};d_{2};d_{3};d_{4};d_{5};d_{6};d_{7};d_{8}$ nằm trên các đường parabol có trục đối xứng song song với SO. Giả sử giao tuyến (nếu có) của $(H)$ với mặt phẳng $(\alpha)$ vuông góc với SO là một bát giác đều và khi $(\alpha)$ đi qua trung điểm của SO thì bát giác đều có cạnh $b = \dfrac{\sqrt{2\sqrt{2} + 4}}{\sqrt{2} + 2}(m)$. Tính thể tích theo đơn vị $m^{3}$ phần không gian nằm bên trong mái chòi $(H)$ (làm tròn kết quả đến hàng phần chục, coi bề dày trần gỗ không đáng kể).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:775990

Phương pháp giải

Tính bán kính đáy và bán kính mặt cắt giữa.

Xác định phương trình parabol.

Ứng dụng tích phân tính thể tích.

Giải chi tiết

Đáy là bát giác đều cạnh $a$, bán kính đường tròn ngoại tiếp $R$, có $a = 2R\sin(\pi/8)$.

Với $a = \dfrac{3\sqrt{2\sqrt{2} + 4}}{\sqrt{2} + 2}$, suy ra $R = 3$ m.

Mặt cắt tại $z = h/2 = 3$ là bát giác đều cạnh $b = \dfrac{\sqrt{2\sqrt{2} + 4}}{\sqrt{2} + 2}$.

$b = 2R_{M}\sin(\pi/8)$, với $R_{M}$ là bán kính mặt cắt giữa.

Do $a = 3b$, suy ra $R = 3R_{M}$. Với $R = 3$, ta có $R_{M} = 1$ m.

Các cạnh bên là parabol $z = Ar^{2} + Br + C$ đi qua các điểm $(r,z)$ là

$(R,0) = (3,0)$, $(0,h) = (0,6)$ và $(R_{M},h/2) = (1,3)$.

Từ $\left. (0,6)\Rightarrow C = 6 \right.$. Từ $(3,0)$ và $(1,3)$ giải hệ:

$\left. \left\{ \begin{array}{l} {9A + 3B + 6 = 0} \\ {A + B + 6 = 3} \end{array} \right.\Rightarrow\left\{ \begin{array}{l} {3A + B = - 2} \\ {A + B = - 3} \end{array} \right.\Rightarrow A = 1/2,B = - 7/2 \right.$.

Vậy $z = \dfrac{1}{2}r^{2} - \dfrac{7}{2}r + 6$.

Giải phương trình bậc hai theo $r$, ta được $r(z) = \dfrac{7 - \sqrt{1 + 8z}}{2}$.

Diện tích mặt cắt ngang tại độ cao $z$ là diện tích bát giác đều bán kính $r(z)$:

$A(z) = 8.\dfrac{1}{2}{\lbrack r(z)\rbrack}^{2}\sin(\pi/4) = 4.{\lbrack r(z)\rbrack}^{2}\dfrac{\sqrt{2}}{2} = 2\sqrt{2}{\lbrack r(z)\rbrack}^{2}$.

$A(z) = 2\sqrt{2}\left( \dfrac{7 - \sqrt{1 + 8z}}{2} \right)^{2} = \dfrac{\sqrt{2}}{2}(50 + 8z - 14\sqrt{1 + 8z})$.

Thể tích cần tính là

$V = {\int_{0}^{6}A}(z)dz = \dfrac{\sqrt{2}}{2}{\int_{0}^{6}{(50 + 8z - 14\sqrt{1 + 8z})}}dz$.

$= \dfrac{\sqrt{2}}{2}\left\lbrack {50z + 4z^{2} - \dfrac{7}{6}{(1 + 8z)}^{3/2}} \right\rbrack_{0}^{6}$$= \dfrac{\sqrt{2}}{2}(444 - 399) = \dfrac{45\sqrt{2}}{2} \approx 31.8$.

Đáp án cần điền là: 31,8

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.