Dựa vào thông tin dưới đây để trả lời các câu sau Một gia đình cần ít nhất 900 đơn
Dựa vào thông tin dưới đây để trả lời các câu sau
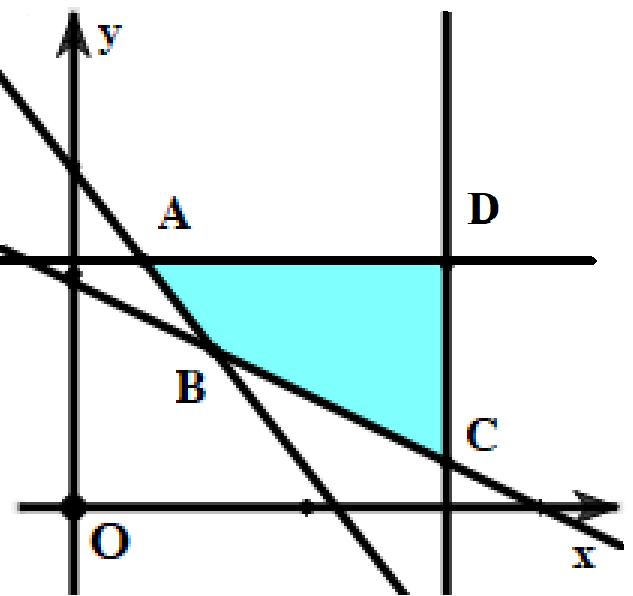
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilogam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, 1 kg thịt lợn là 110 nghìn đồng. Gọi $x,y$(kg) lần lượt là số kg thịt bò và thịt lợn mà gia đình đó đã mua.
Trả lời cho các câu 1, 2 dưới đây:
Điều kiện ràng buộc của bài toán được biểu diễn bởi hệ bất phương trình nào dưới đây?
Đáp án đúng là: A
Lập hệ bất phương trình bậc nhất hai ẩn.
Đáp án cần chọn là: A
Để tổng số tiền gia đình này phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn, giá trị biểu thức $T = x^{2} + y^{2}$ là
Đáp án đúng là: B
Bài toán tối ưu.
Ta có điều kiện ràng buộc của bài toán:
$\left\{ \begin{array}{l} {0 \leq x \leq 1,6} \\ {0 \leq y \leq 1,1} \\ {8x + 6y \geq 9} \\ {x + 2y \geq 2} \end{array} \right.\,\,(*)$.
Biển diễn miền nghiệm của hệ bất phương trình (*) trên mặt phẳng tọa độ $Oxy$, ta được:
Miền nghiệm của hệ bất phương trình (*) là tứ giác $ABCD$, trong đó:
$A\left( {0,3;1,1} \right);B\left( {0,6;0,7} \right);C\left( {1,6;0,2} \right);D\left( {1,6;1,1} \right)$.
Gọi $F$ là tổng số tiền gia đình này phải trả (đơn vị: nghìn đồng) ta có $F = 160x + 110y$. Giá trị của F tại các đỉnh của tứ giác như sau:
Tại $A\left( {0,3;1,1} \right)$: $F = 160.0,3 + 110.1,1 = 169$;
Tại $C\left( {1,6;0,2} \right)$: $F = 160.1,6 + 110.0,2 = 278$;
Tại $B\left( {0,6;0,7} \right)$: $F = 160.0,6 + 110.0,7 = 173$;
Tại $D\left( {1,6;1,1} \right)$: $F = 160.1,6 + 110.1,1 = 377$.
Ta thấy F đạt giá trị nhỏ nhất là $169$ tại $A\left( {0,3;1,1} \right)$.
Do đó, để tổng số tiền gia đình này phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn thì $x = 0,3;y = 1,1$.
Vậy $T = x^{2} + y^{2} = 0,3^{2} + 1,1^{2} = 1,3$.
Đáp án cần chọn là: B
Quảng cáo
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
