Trong môn cầu lông, khi phát cầu, người chơi cần đánh cầu qua khỏi lưới
Trong môn cầu lông, khi phát cầu, người chơi cần đánh cầu qua khỏi lưới sang phía sân đối phương và không được để cho cầu rơi ngoài biên.
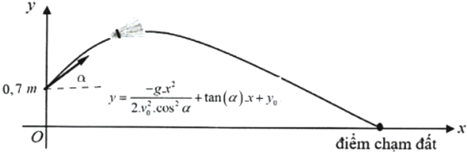
Trong mặt phẳng tọa độ Oxy, chọn điểm có tọa độ \(\left( {O;{y_0}} \right)\) là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời khỏi mặt vợt là:
\[y = \dfrac{{ - g \cdot {x^2}}}{{2 \cdot v_0^2 \cdot {{\cos }^2}\alpha }} + \tan (\alpha ) \cdot x + {y_0}\]
Trong đó:
+) g là gia tốc trọng trường (thường được chọn là \(9,8\;{\rm{m}}/{{\rm{s}}^2}\));
+) \(\alpha \) là góc phát cầu (so với phương ngang của mặt đất);
+) \({v_0}\) là vận tốc ban đầu của cầu;
+) \({y_0}\) là khoảng cách từ vị trí phát cầu đến mặt đất.
Đây là một hàm số bậc hai nên quỹ đạo chuyển động của cầu lông là một parabol.
Một người chơi cầu lông đang đứng khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa) là \(6,68\;{\rm{m}}\), nghĩa là .
Khi đó phương trình quỹ đạo của cầu là .
Biết cầu rời mặt vợt ở độ cao \(0,7\;{\rm{m}}\) so với mặt đất và vận tốc xuất phát của cầu là \(8\;{\rm{m}}/{\rm{s}}\), bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng phẳng đứng.
Người chơi đã phát cầu một góc gần \({54^\circ }\) hoặc gần so với mặt đất.
Đáp án đúng là: \(x = 6,68\;{\rm{m}}\); \(\dfrac{{ - 9,8 \cdot {{(6,68)}^2}}}{{128 \cdot {{\cos }^2}\alpha }} + \tan (\alpha ) \cdot (6,68) + 0,7 = 0\); \({30^\circ }\)
Quảng cáo
Bài toán mô hình hoá chuyển động bằng hàm bậc hai, thay số vào phương trình chuyển động.
Giải phương trình lượng giác bằng cách đặt ẩn phụ.
Đáp án cần chọn là: \(x = 6,68\;{\rm{m}}\); \(\dfrac{{ - 9,8 \cdot {{(6,68)}^2}}}{{128 \cdot {{\cos }^2}\alpha }} + \tan (\alpha ) \cdot (6,68) + 0,7 = 0\); \({30^\circ }\)
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
