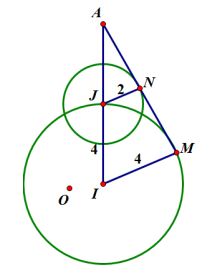
Ở trung tâm nghiên cứu $X$ có một thiết bị được đặt trên một quả đồi

Câu hỏi số 787195:

Vận dụng cao

Ở trung tâm nghiên cứu $X$ có một thiết bị được đặt trên một quả đồi thuộc vùng núi để đo các thông số về thời tiết khí tượng của vùng đó (nhiệt độ, áp suất khí quyển, độ ẩm, mây, gió, mưa…). Cấu tạo bên ngoài của thiết bị gồm hai mặt cầu cắt nhau là $\left( S_{1} \right)$ có tâm $I$, bán kính bằng $4m$ và mặt cầu $\left( S_{2} \right)$ có tâm $J$, bán kính bằng $2m$. Để đo các thông số cần thiết, người ta lắp đặt một tấm thiết bị điện tử hình chữ nhật $(R)$ luôn tiếp xúc với cả hai mặt cầu $\left( S_{1} \right),\,\,\left( S_{2} \right)$ và có thể di chuyển quanh các chỏm cầu để truyền tín hiệu tới hộp điều hành (đường truyền không dây). Đáp án: hệ trục tọa độ $Oxyz$ trong không gian với độ dài đơn vị trên mỗi trục tọa độ là $1m$ và $O\left( {0;0;0} \right)$ là vị trí hộp điều hành thiết bị thì $I\left( {2;1;1} \right)$ và $J\left( {2;1;5} \right)$. Khi khoảng cách từ $O$ đến tấm thiết bị điện tử $(R)$ ngắn nhất là lúc đường truyền tín hiệu tốt nhất. Khoảng cách ngắn nhất này là bao nhiêu mét? (Kết quả làm tròn đến hàng phần trăm, tham khảo mô tả thiết bị như hình trên).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:787195

Phương pháp giải

Đưa về bài toán hình học không gian tìm vị trí của mặt phẳng để khoảng cách từ 1 điểm đến 1 mặt phẳng là nhỏ nhất.

Giải chi tiết

Ta có: $\left. \overset{\rightarrow}{IJ} = \left( {0;0;4} \right),\,\, IJ = 4\Rightarrow J \in \left( {I;4} \right) \right.$

Và $OI = \sqrt{6} < 4$ nên $O$ nằm trong mặt cầu $\left( S_{1} \right)$

Gọi $M,\,\, N$ là tiếp điểm của tấm thiết bị điện tử hình chữ nhật $(\alpha)$ và hai mặt cầu $\left( S_{1} \right),\,\,\left( S_{2} \right)$

Khi đó $MN$ là tiếp tuyến của 2 mặt cầu và $IM = 4 = 2JN,\,\, IM \parallel JN$

Gọi $A$ là giao điểm của $IJ$ và $MN$

Trong $\Delta AIM$ có $JN \parallel IM$ và $N$ là trung điểm của $AM$ khi đó $J$ là trung điểm của $AI$

Khi đó $A\left( {2;1;9} \right)$

Gọi $\varphi$ là góc giữa $IJ$ và $MN$

$\left. \Rightarrow\sin\varphi = \dfrac{JN}{AJ} = \dfrac{1}{2}\Rightarrow\varphi = 30{^\circ} \right.$

Vì $MN$ là hình chiếu của $IJ$ trên $(\alpha)$ nên $\varphi$ cũng là góc giữa $IJ$ và $(\alpha)$

Bài toán trở thành: Mặt phẳng $(\alpha)$ thay đổi luôn đi qua $A\left( {2;1;9} \right)$, tạo với đường thẳng $AI$ một góc không đổi $\varphi = 30{^\circ}$. Tìm khoảng cách ngắn nhất từ gốc $O$ đến mặt phẳng $(\alpha)$

Ta có: $\overset{\rightarrow}{AO} = \left( {- 2; - 1; - 9} \right),\,\,\overset{\rightarrow}{AI} = \left( {0;0; - 8} \right)$

$\left. \Rightarrow\cos\angle OAI = \cos\left( {AO;AI} \right) = \dfrac{9}{\sqrt{86}}\Rightarrow\angle OAI \approx 13,95{^\circ} \right.$

Gọi $H$ là hình chiếu vuông góc của $O$ trên mặt phẳng $(\alpha)$

Ta có $d\left( {O;(\alpha)} \right) = OH = AO.\sin\angle OAH = \sqrt{86}.\sin\angle OAH$

Lại có: $\left. \angle OAH + \angle OAI \geq \angle HAI \geq \angle MAI = 30{^\circ}\Leftrightarrow OAH \geq 30{^\circ} - \angle OAI \approx 16,05{^\circ} \right.$

Dấu $" = "$ xảy ra khi và chỉ khi $O,\,\, I,\,\, H$ thẳng hàng hay $H \equiv M$

$d\left( {O,(\alpha)} \right) = \sqrt{86}.\sin\angle OAH \geq \sqrt{86}.\sin 16,05{^\circ} \approx 2,56$

Đáp án cần điền là: 2,56

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.