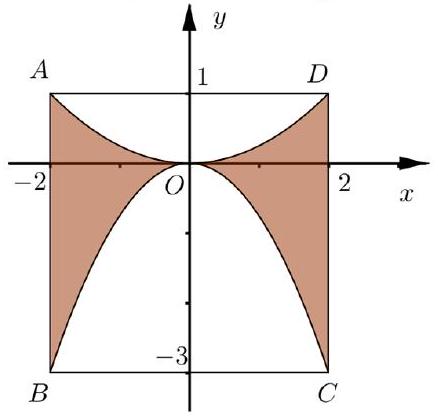
Một công ty thiết kế mẫu huy hiệu để tặng cho khách hàng thân thiết của
Một công ty thiết kế mẫu huy hiệu để tặng cho khách hàng thân thiết của mình (xem hình bên). Trong đó $ABCD$ là hình vuông có cạnh bằng 4 cm , các đường cong $AOD$ và $BOC$ là một phần của các parabol đỉnh $O$. Với hệ trục tọa độ $Oxy$ (đơn vị trên mỗi trục tọa độ là centimét) thì điểm $A$ có tung độ bằng 1. Biết phần tô đậm trong hình vẽ được phủ vàng với chi phí 1 triệu đồng$/1\text{cm}^{2}$, phần còn lại được phủ bạc với chi phí 300 nghìn đồng $/\text{cm}^{2}$, các chi phí còn lại là 500 nghìn đồng.
| Đúng | Sai | |
|---|---|---|
| a) Parabol chứa đường cong $AOD$ có phương trình là $y = \dfrac{1}{16}x^{2}$. | ||
| b) Parabol chứa đường cong $BOC$ có phương trình là $y = - \dfrac{3}{4}x^{2}$. | ||
| c) Diện tích phần tô đậm trong hình vẽ lớn hơn $5,5\text{cm}^{2}$. | ||
| d) Chi phí sản xuất một chiếc huy hiệu như trên nhỏ hơn 9 triệu đồng. |
Đáp án đúng là: S; Đ; S; S
Quảng cáo
Gắn hệ trục toạ độ Oxy. Xác định toạ độ các điểm và các hàm số từ đó tính diện tích bằng tích phân
a) Sai. Theo giả thiết, Parabol chứa đường cong $AOD$ có đỉnh $O$, nhận $Oy$ làm trục đối xứng và đi qua điểm $A\left( {- 2;1} \right)$ nên có phương trình $y = \dfrac{1}{4}x^{2}$.
b) Đúng. Theo giả thiết, Parabol chứa đường cong $BOC$ có đỉnh $O$, nhận $Oy$; làm trục đối xứng và đi qua điểm $A\left( {- 2; - 3} \right)$ nên có phương trình $y = - \dfrac{3}{4}x^{2}$.
c) Sai. Diện tích phần tô đậm trong hình vẽ là
$S = 2\int_{0}^{2}\left( {\dfrac{1}{4}x^{2} + \dfrac{3}{4}x^{2}} \right)\text{d}x = 2\int_{0}^{2}x^{2}\text{d}x = \left. {\dfrac{2}{3}x^{3}} \right|_{0}^{2} = \dfrac{16}{3}y = \left( \text{cm}^{2} \right)$.
Ta thấy $\dfrac{16}{3} < 5,5.$
d) Sai. Diện tích hình vuông $ABCD$ là $16\text{cm}^{2}$. Diện tích phần phủ vàng là $\dfrac{16}{3}\left( \text{cm}^{2} \right)$, diện tích phần phủ bạc là $16 - \dfrac{16}{3} = \dfrac{32}{3}\left( \text{cm}^{2} \right)$.
Vậy chi phí để làm chiếc huy hiệu là $500000 + \dfrac{16}{3} \cdot 1000000 + \dfrac{32}{3} \cdot 300000 = \dfrac{27100000}{3} \simeq 9033333\ $(đồng)
Chi phí trên lớn hơn 9 triệu đồng.
Đáp án cần chọn là: S; Đ; S; S
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
