Việc lắp đặt các trạm BTS để thu phát sóng và kết nối thông tin, nếu khoảng cách 2 trạm
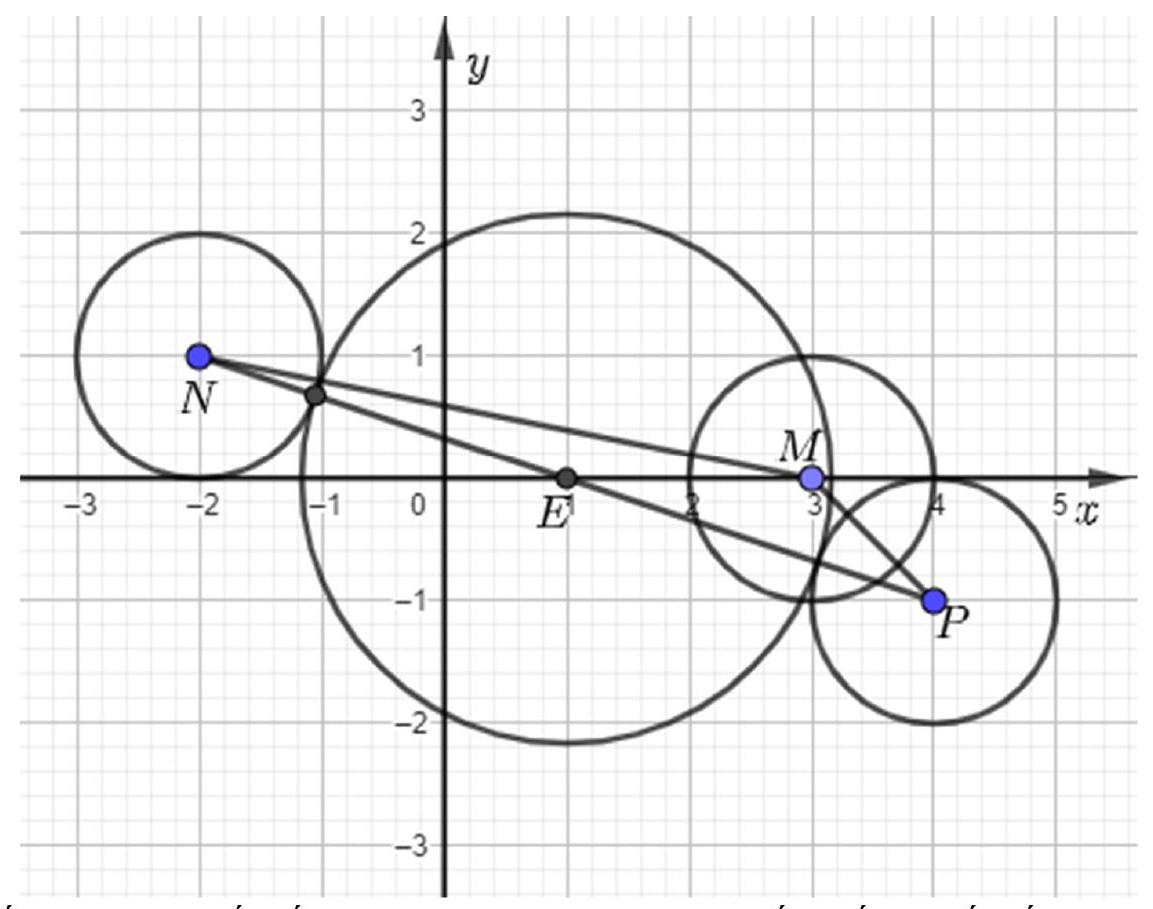
Việc lắp đặt các trạm BTS để thu phát sóng và kết nối thông tin, nếu khoảng cách 2 trạm luôn nhỏ hơn hoặc bằng tổng hai bán kính phủ sóng của hai trạm đó thì chúng luôn kết nối thông tin được với nhau. Giả sử trong không gian với hệ trục Oxyz , có 3 trạm thu phát sóng lần lượt đặt tại các vị trí là điểm $M\left( {0;3; - 1} \right),N\left( {- 2;1; - 1} \right),P\left( {4; - 1; - 1} \right)$, đồng thời các trạm này có bán kính phủ sóng bằng nhau là 1. Người ta muốn đặt thêm một trạm thu phát sóng tại vị trí $E\left( {a;b;c} \right)$, sao cho bán kính phủ sóng tại đây nhỏ nhất là R và vừa đủ để kết nối được hết cả 3 trạm đã đặt trước đó. Tính ${(R + 2a - 2b + c)}^{2}$.
Đáp án đúng là:
Quảng cáo
Chiếu xuống (Oxy) từ đó suy ra E là trung điểm NP
Để bán kính R nhỏ nhất điều kiện cần là $\left. E \in \left( {MNP} \right)\Rightarrow c = - 1 \right.$.
Do phương trình $\left( {MNP} \right)$ là $z = - 1$ nên chiếu lên mặt phẳng $Oxy$ ta được
Nhận xét nếu trạm tại E kết nối được với trạm tại $\text{N},\text{P}$ thì chắc chắn sẽ kết nối được với trạm tại P.
Để bán kính R nhỏ nhất, thì $E\left( {1;0; - 1} \right)$ là trung điểm của NP và $R = \dfrac{NP - 2}{2} = \sqrt{10} - 1$.
${(R + 2a - 2b + c)}^{2} = 10$.
Đáp án cần điền là: 10
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
