Trong một cuộc thi sáng tạo các chủ đề liên quan đến Kỷ niệm 50 năm ngày miền Nam hoàn toàn
Trong một cuộc thi sáng tạo các chủ đề liên quan đến Kỷ niệm 50 năm ngày miền Nam hoàn toàn giải phóng, tại hệ thống trường Nguyễn Khuyến, Lê Thánh Tông, một em học sinh đến từ lớp 12B1 đã đạt giải đặc biệt với một thiết kế vô cùng độc đáo. Em học sinh này đã thiết kế bề mặt của một chiếc đồng hồ treo tường bằng sự kết hợp giữa lịch sử, mỹ thuật và toán học.
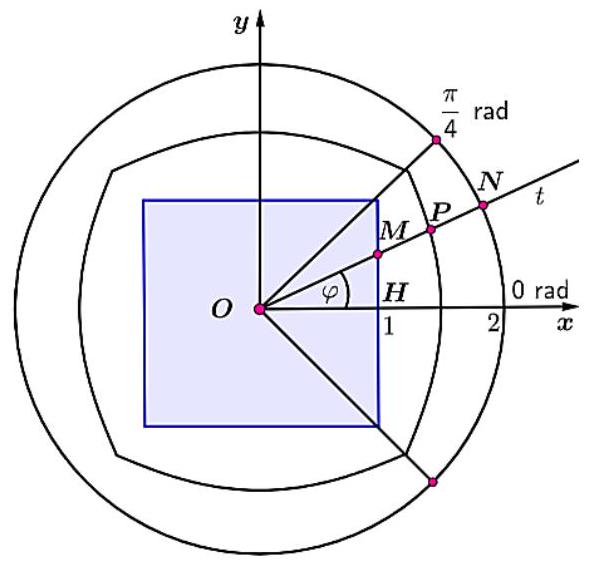
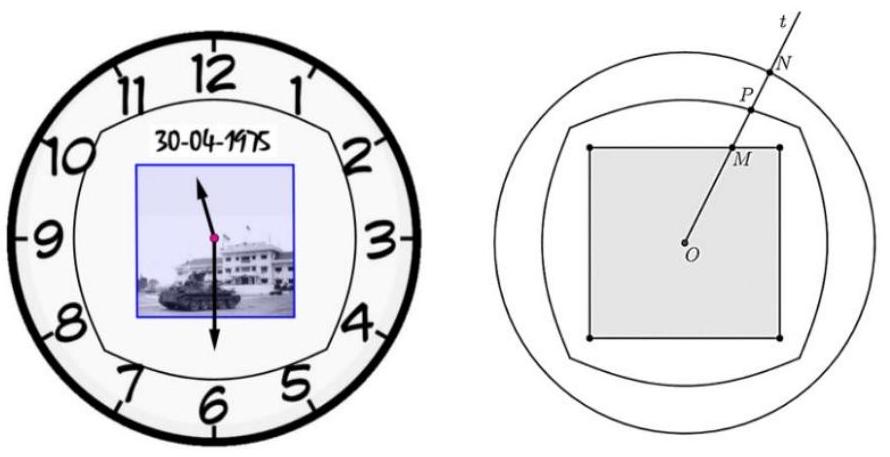
- Phần trong của mặt đồng hồ là hình vuông có cạnh bằng 2 dm, nơi đây lưu giữ hình ảnh của chiếc xe tăng 390 của bộ đội Việt Nam tiến vào dinh độc lập.
- Phần ngoài của mặt đồng hồ là đường tròn có bán kính bằng 2 dm.
- Đường cong trung gian có tên $(L)$ là tập hợp tất cả điểm $P$ sao cho nếu kẻ tia $Ot$ bất kỳ cắt hình vuông và đường tròn lần lượt tại $M,N$ thì $P$ là trung điểm $MN$ ($O$ là tâm đường tròn). Tìm diện tích hình phẳng giới hạn bởi đường cong $(L)$ theo đơn vị $dm^{2}$ và làm tròn đến hàng phần trăm.
Đáp án đúng là:
Quảng cáo
Xác định phương trình đường cong $(L)$ chứa điểm P từ đó tính diện tích bằng tích phân.
Xét hình vẽ sau với $O$ là tâm hình vuông và tia $Ox$ đi qua trung điểm $H$ của một cạnh hình vuông, gọi $\varphi$ là góc hợp bởi tia $Ox$ và tia $Ot$ với $\varphi \in \left\lbrack {0;\dfrac{\pi}{4}} \right\rbrack$.
Ta có $\left. M\left( {1,\tan\varphi} \right);N\left( {2\cos\varphi,2\sin\varphi} \right)\Rightarrow P\left( {\dfrac{1 + 2\cos\varphi}{2};\dfrac{\tan\varphi + 2\sin\varphi}{2}} \right) \right.$
Đặt $\left. x = \dfrac{1 + 2\cos\varphi}{2}\Leftrightarrow\cos\varphi = \dfrac{2x - 1}{2} \right.$. Với $\varphi \in \left\lbrack {0;\dfrac{\pi}{4}} \right\rbrack$ thì $x \in \left( {\dfrac{1 + \sqrt{2}}{2};\dfrac{3}{2}} \right)$
$\left. \Rightarrow\dfrac{\tan\varphi + 2\sin\varphi}{2} = \dfrac{\sin\varphi + 2\sin\varphi.\cos\varphi}{2\cos\varphi} = \dfrac{\sin\varphi.2x}{2x - 1} = \dfrac{2x}{2x - 1}.\sqrt{1 - \left( \dfrac{2x - 1}{2} \right)^{2}} \right.$
Vậy P luôn thuộc đường cong $y = \dfrac{2x}{2x - 1}.\sqrt{1 - \left( \dfrac{2x - 1}{2} \right)^{2}}$ với $x \in \left( {\dfrac{1 + \sqrt{2}}{2};\dfrac{3}{2}} \right)$
Vậy diện tích của đường cong $(L)$ là: $S = 8\left\lbrack {{\int\limits_{0}^{\dfrac{1 + \sqrt{2}}{2}}x}dx + {\int\limits_{\dfrac{1 + \sqrt{2}}{2}}^{\dfrac{3}{2}}{\dfrac{2x}{2x - 1}.\sqrt{1 - \left( \dfrac{2x - 1}{2} \right)^{2}}}}dx} \right\rbrack \approx 7,67$
Đáp án cần điền là: 7,67
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
