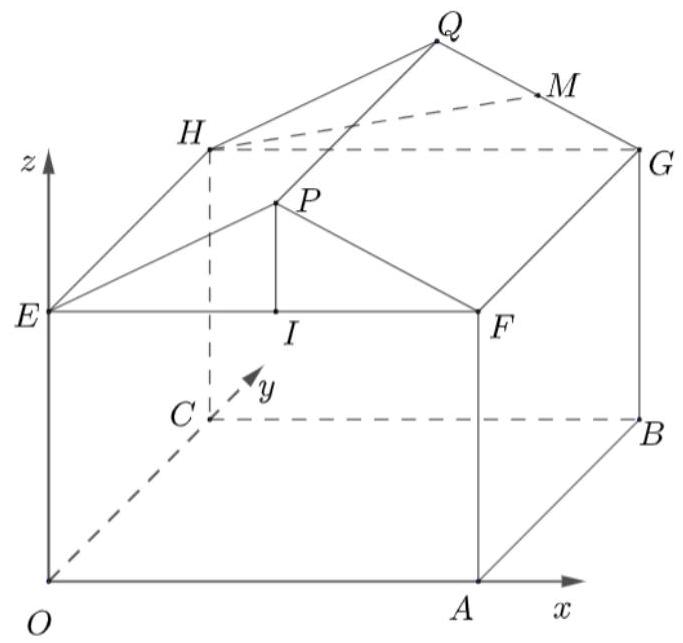
Một kho chứa hàng có hình dạng là khối đa diện $OAFPECBGQH$, trong đó $OABC.EFGH$ là một khối
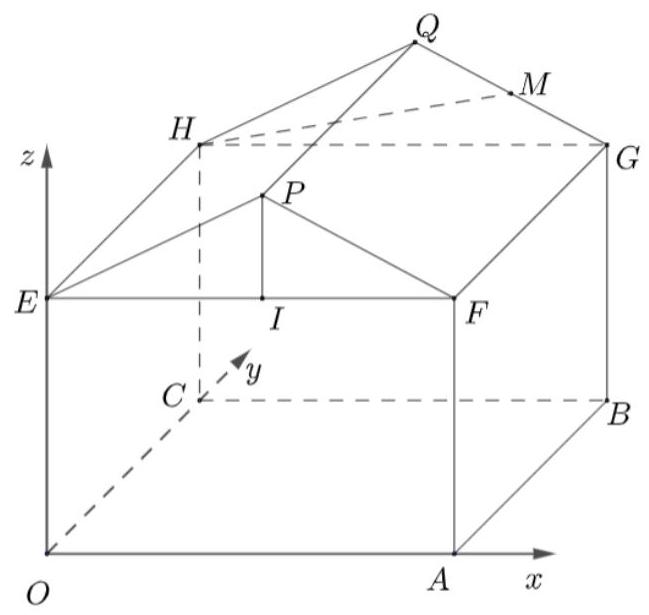
Một kho chứa hàng có hình dạng là khối đa diện $OAFPECBGQH$, trong đó $OABC.EFGH$ là một khối hộp chữ nhật, $EFP$ là tam giác cân tại $P$, tam giác $HGQ$ cân tại $Q$ và bằng tam giác $EFP$. Biết $OA = 4m;AB = 6m;HC = 5m$; độ dốc của mái nhà, tức là số đo góc nhị diện $\left\lbrack {Q,FG,H} \right\rbrack$ bằng $45^{\circ}$. Người ta mô hình hóa nhà kho bằng cách chọn hệ trục tọa độ tương ứng như hình vẽ bên (đơn vị trên mỗi trục là $1m)$.
| Đúng | Sai | |
|---|---|---|
| a) Tọa độ của $\overset{\rightarrow}{PQ}$ là $\left( {0;6;0} \right)$. | ||
| b) Tọa độ của điểm $G$ là $\left( {6;4;5} \right)$. | ||
| c) Chiều cao kho hàng tức là khoảng cách từ nóc nhà (điểm cao nhất của nóc nhà) và sàn nhà bằng 7 m . | ||
| d) Người ta muốn lắp camera quan sát trong nhà kho tại vị trí trung điểm $M$ của $GQ$ và đầu thu dữ liệu đặt tại vị trí $O$. Người ta thiết kế đường dây cáp nối từ $O$ đến $E$ rồi từ $E$ đến $H$ và từ $H$ đến $M$. Độ dài đoạn cáp nối tối thiểu bằng $11 + \sqrt{10}m$. |
Đáp án đúng là: Đ; S; Đ; Đ
Quảng cáo
Từ độ dài các cạnh xác định toạ độ các điểm từ đó tính góc nhị diện và độ dài các cạnh
a) Đúng. Ta có $A\left( {4;0;0} \right),B\left( {4;6;0} \right),C\left( {0;6;0} \right),H\left( {0;6;5} \right)$.
Vì $P,Q$ có cùng cao độ và hoành độ, $PQ = AB = 6m$ nên $\overset{\rightarrow}{PQ} = \left( {0;6;0} \right)$
b) Sai. Ta có $A\left( {4;0;0} \right),B\left( {4;6;0} \right),C\left( {0;6;0} \right),H\left( {0;6;5} \right)$.
Suy ra $G\left( {4;6;5} \right)$.
c) Đúng. Gọi $I$ là trung điểm của $EF$.
Vì $\Delta EFP$ cân tại $P$ nên $PI$ là đường cao.
Khoảng cách giữa nóc nhà và sàn nhà là $PI + FA = PI + 5\left( \text{m} \right)$
Vì $QG\bot FG,HG\bot FG$ nên số đo góc nhị diện $\left\lbrack {Q,FG,H} \right\rbrack$ là $\widehat{QGH} = 45^{\circ}$.
Suy ra $\widehat{PFE} = 45^{\circ}$.
Suy ra $\Delta EFP$ vuông cân tại $P$. Suy ra $PI = \dfrac{1}{2}EF = \dfrac{1}{2} \cdot 4 = 2\left( \text{~m} \right)$
Vậy khoảng cách giữa nóc nhà và sàn nhà là $7m$.
d) Đúng. Xét $\Delta QHG$ vuông cân tại $Q$ có $HQ = QG = \dfrac{HG}{\sqrt{2}} = \dfrac{4}{\sqrt{2}} = 2\sqrt{2}\left( \text{m} \right)$.
Gọi $M$ là trung điểm của $GQ$ suy ra $QM = \sqrt{2}(m)$.
Xét $\Delta QHM$ vuông tại $Q$ có $HM^{2} = QM^{2} + HQ^{2}$ suy ra $HM = \sqrt{{(2\sqrt{2})}^{2} + {(\sqrt{2})}^{2}} = \sqrt{10}(m)$.
Suy ra độ dài đoạn cáp nối tối thiểu bằng $OE + EH + HM = 5 + 6 + \sqrt{10} = 11 + \sqrt{10}\left( \text{~m} \right)$.
Đáp án cần chọn là: Đ; S; Đ; Đ
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
