Hệ thống định vị toàn cầu GPS (Global Positioning System) là một hệ thống cho phép xác định
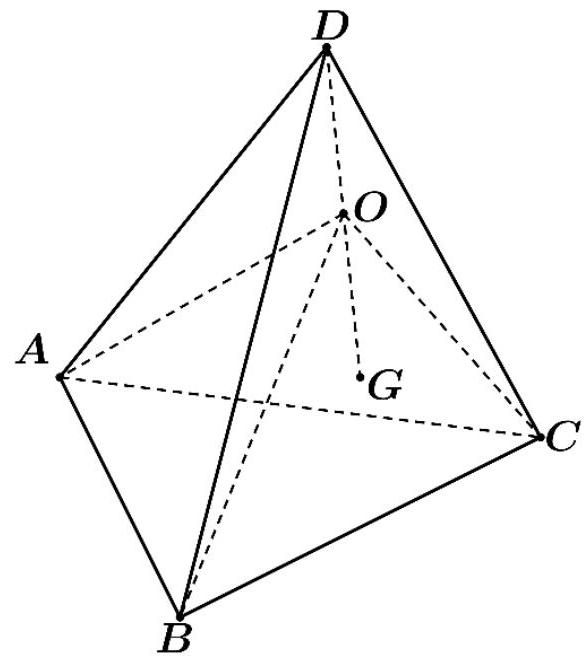
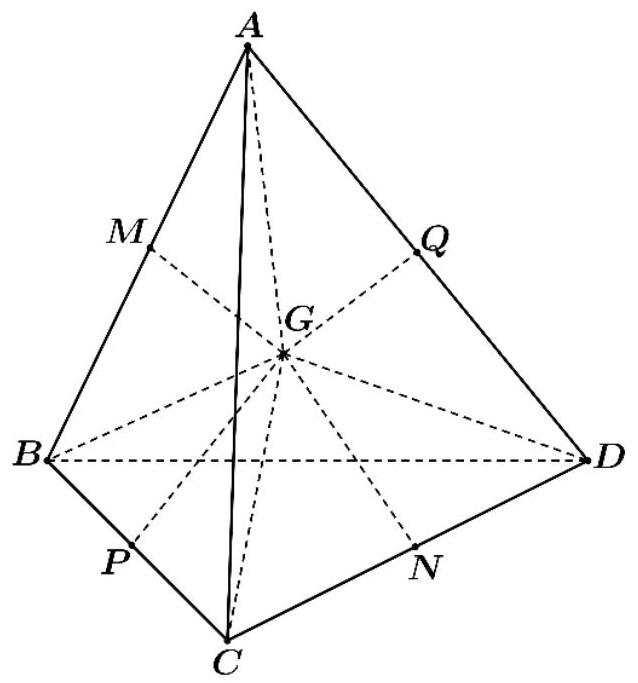
Hệ thống định vị toàn cầu GPS (Global Positioning System) là một hệ thống cho phép xác định vị trí của một vật thể trong không gian. Trong cùng một thời điểm vị trí của một điểm $M$ trong không gian sẽ được xác định bởi bốn vệ tinh cho trước nhờ các bộ thu phát tín hiệu đặt trên các vệ tinh đó. Giả sử trong không gian với hệ trục tọa độ $Oxyz$, có bốn vệ tinh lần lượt đặt tại các điểm $A\left( {2;4;0} \right),B\left( {0;4;6} \right),C\left( {2;0;6} \right),D\left( {- 1; - 2; - 3} \right)$ và vị trí của điểm $M\left( {a;b;c} \right)$ thỏa mãn biểu thức $MA + MB + MC + MD$ nhỏ nhất. Tính độ dài $MO$ (Kết quả làm tròn đến hàng phần chục)
Đáp án đúng là:
Quảng cáo
Gọi G là trọng tâm tứ diện. Suy ra: $MA + MB + MC + MD \geq GA + GB + GC + GD$
Dấu bằng xảy ra khi $M \equiv G$.
Cách 1: Cho tứ diện $ABCD$ và $I$ là điểm thỏa mãn $AIB = CID,AIC = BID$ và $AID = BIC$ thì với mọi điểm $M$ nằm trong không gian ta có: $MA + MB + MC + MD \geq IA + IB + IC + ID$
Dấu bằng xảy ra khi $M \equiv I$.
Ta có tứ diện $OABC$ là tứ diện gần đều $OA = BC,OB = AC,OC = AB$.
Gọi $G\left( {1;2;3} \right)$ là trọng tâm của tứ diện $OABC$, dễ thấy $O$ là trung điểm của $DG$
Khi đó ta có được: $AGB = CGD,AGC = BGD$ và $AGD = BGC$.
Suy ra: $MA + MB + MC + MD \geq GA + GB + GC + GD$
Dấu bằng xảy ra khi $\left. M \equiv G\Rightarrow M\left( {1;2;3} \right)\Rightarrow OM = \sqrt{14} \approx 3,7 \right.$.
Cách 2: Gọi $G$ là trọng tâm của tứ diện; $M,N,P,Q$ lần lượt là trung điểm của các cạnh $AB$, $CD,BC,AD$.
Ta có $\Delta ACD = \Delta BDC$ nên $AN = BN$ suy ra $MN\bot AB$.
Tương tự ta chứng minh được $MN\bot CD$ và đường thẳng $PQ$ vuông góc với cả hai đường thẳng $AD,BC$.
Từ đó suy ra $GA = GB = GC = GD$
Ta có: $XA + XB + XC + XD = \dfrac{XA \cdot GA + XB \cdot GB + XC \cdot GC + XD \cdot GD}{GA}$
$\begin{array}{l} {\geq \dfrac{\overset{\rightarrow}{XA} \cdot \overset{\rightarrow}{GA} + \overset{\rightarrow}{XB} \cdot \overset{\rightarrow}{GB} + \overset{\rightarrow}{XC} \cdot \overset{\rightarrow}{GC} + \overset{\rightarrow}{XD} \cdot \overset{\rightarrow}{GD}}{\overset{\rightarrow}{GA}}} \\ {= \dfrac{\overset{\rightarrow}{XG}\left( {\overset{\rightarrow}{GA} + \overset{\rightarrow}{GB} + \overset{\rightarrow}{GC} + \overset{\rightarrow}{GD}} \right) + 4GA^{2}}{GA} = 4GA} \end{array}$
Dấu bằng xảy ra khi và chỉ khi $X$ trùng với điểm $G$.
Đáp án cần điền là: 3,7
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
