Nguồn sáng phát ra từ một cây đèn pin khi chiếu vào một quả cầu phản quang sẽ cho ta hình
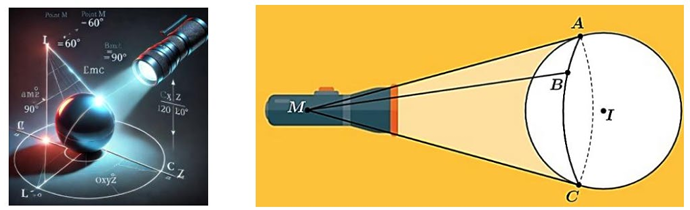
Nguồn sáng phát ra từ một cây đèn pin khi chiếu vào một quả cầu phản quang sẽ cho ta hình ảnh của một mặt cầu tiếp xúc với các đường sinh của một hình nón (xem hình vẽ). giả sử nguồn sáng phát ra từ điểm M, trong một hệ trục tọa độ Oxyz cho sẵn với đơn vị trên mỗi trục là mét, các tiếp tuyến MA, MB, MC thoả mãn $AMB = 60^{{^\circ}},BMC = 90^{{^\circ}},CMA = 120^{{^\circ}}$. Mặt cầu $(S)$ có phương trình $x^{2} + y^{2} + z^{2} - 2x - 4y + 6z - 13 = 0$
| Đúng | Sai | |
|---|---|---|
| a) Mặt cầu (S) có tâm $I(1;2; - 3)$ và bán kính $R = 3\sqrt{3}$. | ||
| b) Nếu đặt $MA = MB = MC = x > 0$ thì $AB = x,BC = x\sqrt{3},AC = x\sqrt{2}$ | ||
| c) Tam giác ABC cân. | ||
| d) Độ dài bé nhất của OM là 2,26 (kết quả được làm tròn đến hàng phần trăm). |
Đáp án đúng là: Đ; S; S; Đ
Quảng cáo
a) Mặt cầu tâm $I\left( {a,b,c} \right)$ bán kính R có phương trình $\left( {x - a} \right)^{2} + \left( {y - b} \right)^{2} + \left( {z - c} \right)^{2} = R^{2}$
b) Tính AB, BC, CA bằng định lý cosin
c) Kiểm tra bằng định lý pytago
d) Ta có $MO + OI \geq MI$. Đẳng thức xảy ra khi M, O, I thẳng hàng.
Đáp án cần chọn là: Đ; S; S; Đ
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
