Cho một cái màn chụp tự bung được làm từ hai khung thép, mỗi khung thép là một nửa elip nằm

Câu hỏi số 805476:

Vận dụng

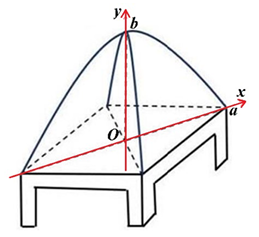
Cho một cái màn chụp tự bung được làm từ hai khung thép, mỗi khung thép là một nửa elip nằm trên hai mặt phẳng vuông góc với mặt giường. Hai khung thép đó giao nhau tại đỉnh màn và là đỉnh của hai nửa elip đó. Cái màn được đặt vừa vặn lên mặt giường hình chữ nhật dài 2m và rộng 1,8m. Khoảng cách từ đỉnh màn xuống mặt giường là 1,2m (tham khảo hình bên). Tính thể tích của phần không gian bên trong màn theo đơn vị m³ (làm tròn kết quả đến hàng phần mười).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:805476

Phương pháp giải

Mặt cắt ngang cái màn chụp theo mặt phẳng song song với mặt giường luôn luôn là một hình chữ nhật nên ta gắn hệ trục toạ độ với O là tâm bàn, hai trục Ox, Oy là hai đường chéo và đường thẳng nối từ đỉnh màn tới O.

Xác định phương trình elip để tính diện tích mặt cắt từ đó tính thể tích bằng tích phân.

Giải chi tiết

Mặt cắt ngang cái màn chụp theo mặt phẳng song song với mặt giường luôn luôn là một hình chữ nhật.

Mặt giường là một hình chữ nhật có đường chéo bằng: $\sqrt{1,8^{2} + 2^{2}} = \dfrac{\sqrt{181}}{5}\text{m}$.

$\dfrac{\sqrt{181}}{5}:2 = \dfrac{\sqrt{181}}{10} \approx 1,3 > 1,2\text{m}$

Từ đó ta lắp hệ trục Oxy như hình minh họa sau:

Trong đó: $a = \dfrac{\sqrt{181}}{10};b = 1,2$.

Phương trình chính tắc elip: $\left. \dfrac{x^{2}}{a^{2}} + \dfrac{y^{2}}{b^{2}} = 1\Leftrightarrow x = \pm a \cdot \sqrt{1 - \dfrac{y^{2}}{b^{2}}} \right.$.

Khi đó: đường chéo của mặt cắt hình chữ nhật bằng $2a \cdot \sqrt{1 - \dfrac{y^{2}}{b^{2}}} = t$.

Tỉ lệ chiều rộng chia chiều dài của hình chữ nhật: $\left. \dfrac{m}{n} = \dfrac{1,8}{2}\Leftrightarrow m = 0,9n \right.$.

Ta có: $\left. m^{2} + n^{2} = t^{2}\Leftrightarrow{(0,9n)}^{2} + n^{2} = t^{2}\Leftrightarrow n = \dfrac{10}{\sqrt{181}}.t\Rightarrow m = \dfrac{9}{\sqrt{181}}.t \right.$

Diện tích mặt cắt: $S(y) = \dfrac{10}{\sqrt{181}}t \cdot \dfrac{9}{\sqrt{181}}t = \dfrac{90}{181}t^{2} = \dfrac{90}{181} \cdot 4a^{2}\left( {1 - \dfrac{y^{2}}{b^{2}}} \right) = \dfrac{18}{5} \cdot \left( {1 - \dfrac{y^{2}}{1,44}} \right)$.

Thể tích của phần không gian bên trong màn:

$V = {\int_{0}^{1,2}S}(y)\text{d}y = {\int_{0}^{1,2}\dfrac{18}{5}} \cdot \left( {1 - \dfrac{y^{2}}{1,44}} \right)\text{d}y = \dfrac{72}{25} = 2,88 \approx 2,9~\text{m}^{3}$

Đáp án cần điền là: 2,9

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.