Xét một hệ trục tọa độ Oxyz được cho sẵn, đơn vị trên mỗi trục là dm,
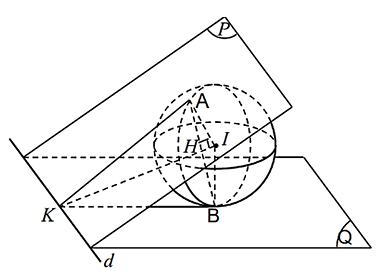
Xét một hệ trục tọa độ Oxyz được cho sẵn, đơn vị trên mỗi trục là dm, mặt ngoài của một quả bóng được mô hình hóa bởi phương trình mặt cầu ${(x - 2)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 6$, quả bóng nằm yên trên sàn nhà. Người ta nhìn thấy một tấm ván ngã xuống đè lên quả bóng, phần giao của tấm ván và sàn nhà là đường thẳng d có phương trình $\dfrac{x + 2}{2} = \dfrac{y + 1}{- 3} = \dfrac{z}{1}$. Gọi A, B lần lượt là tiếp điểm của tấm ván và sàn nhà với quả bóng, I là tâm quả bóng.
| Đúng | Sai | |
|---|---|---|
| a) Quả bóng có tâm $I(2; - 1; - 1)$ và bán kính $R = \sqrt{6}$. | ||
| b) Khoảng cách từ tâm quả bóng đến đường thẳng d bằng $2\sqrt{6}$. | ||
| c) Nếu $\cos AIB$ bằng $\dfrac{a}{b}$ (phân số tối giản) thì giá trị $a^{2} + b^{2} = 82$. | ||
| d) Một con kiến bò từ vị trí A đến vị trí B trên quả bóng với tốc độ $2\text{cm}/\text{s}$; thời gian ngắn nhất cho chuyến đi này là 21 giây (làm tròn đến hàng đơn vị). |
Đáp án đúng là: Đ; S; Đ; S
Quảng cáo
a) Phương trình đường tròn $\left( {x - a} \right)^{2} + \left( {y - b} \right)^{2} + \left( {z - c} \right)^{2} = R^{2}$ có tâm $I\left( {a,b,c} \right)$ và bán kính $R$
b) Áp dụng công thức tính khoảng cách $d\left( {I,d} \right) = \dfrac{\left\lbrack {\overset{\rightarrow}{IA},\overset{\rightarrow}{u}} \right\rbrack}{\left| \overset{\rightarrow}{u} \right|}$ với $A \in d$
c) $\cos AIB = 2\cos^{2}AIK - 1$
d) Kiến bò quãng đường ngắn nhất khi đi trên cung tròn nhỏ AB từ đó tính quãng đường và thời gian.
a) Đúng. Mặt ngoài quả bóng là mặt cầu $(S)$ có tâm $I(2; - 1; - 1)$ và bán kính $R = \sqrt{6}$.
b) Sai. Đường thẳng $d:\dfrac{x + 2}{2} = \dfrac{y + 1}{- 3} = \dfrac{z}{1}$ qua $A( - 2; - 1;0)$ và có vectơ chỉ phương ${\overset{\rightarrow}{u}}_{d} = (2; - 3;1)$.
Ta có: $\overset{\rightarrow}{AI} = (4;0; - 1);\left\lbrack {{\overset{\rightarrow}{u}}_{d},\overset{\rightarrow}{AI}} \right\rbrack = (3;6;12)$.
Do đó $d(I,d) = \dfrac{\left| \left\lbrack {{\overset{\rightarrow}{u}}_{d},\overset{\rightarrow}{AI}} \right\rbrack \right|}{\left| {\overset{\rightarrow}{u}}_{d} \right|} = \dfrac{\sqrt{3^{2} + 6^{2} + 12^{2}}}{\sqrt{2^{2} + {( - 3)}^{2} + 1^{2}}} = \dfrac{3\sqrt{6}}{2}$.
c) Đúng. Gọi K là hình chiếu của I trên d thì $KI = \dfrac{3\sqrt{6}}{2}$ và $KA\bot IA$
$\left. \Rightarrow\cos AIK = \dfrac{IA}{IK} = \dfrac{2}{3} \right.$.
Do vậy $\left. \cos AIB = 2\cos^{2}AIK - 1 = 2.\left( \dfrac{2}{3} \right)^{2} - 1 = - \dfrac{1}{9} = \dfrac{a}{b}\Rightarrow a^{2} + b^{2} = 82 \right.$
d) Sai. Ta có $\left. \cos AIB = - \dfrac{1}{9}\Rightarrow\angle AIB = 96,38^{0} \right.$
Độ dài cung tròn bé nhất mà con kiến có thể đi: $l_{AB} = \dfrac{\pi R.\angle AIB}{180} = \sqrt{6}\pi.\dfrac{96,38}{180} \approx 4,12\text{dm}$.
Thời gian tối thiểu để kiến đến nơi là $\dfrac{I_{AB}.10}{2} \approx 21$ giây.
Đáp án cần chọn là: Đ; S; Đ; S
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
