Một tay lái mô tô nặng 180 (lb), di chuyển với vận tốc không đổi 30

Câu hỏi số 810558:

Thông hiểu

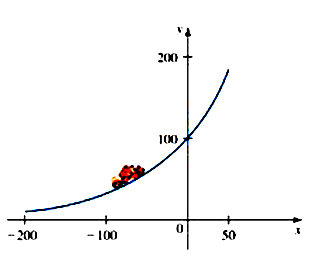
Một tay lái mô tô nặng 180 (lb), di chuyển với vận tốc không đổi 30 dặm/giờ, thực hiện một khúc cua trên đường cho bởi đồ thị $y = 100e^{0,01x}, - 200 \leq x \leq 50$. Có thể chứng minh rằng độ lớn của lực pháp tuyến tác dụng lên tay lái mô tô xấp xỉ $F(x) = \dfrac{10890e^{0,1x}}{\left( {1 + 100e^{0,2x}} \right)^{\dfrac{3}{2}}}$ (đơn vị lb). Hãy tìm lực pháp tuyến lớn nhất tác dụng lên tay lái trong suốt khúc cua (làm tròn kết quả đến hàng đơn vị).

Đáp án:

Đáp án đúng là: 419

Quảng cáo

Xem lời giải

Câu hỏi:810558

Phương pháp giải

Tính đạo hàm và tìm GTLN

Giải chi tiết

$\begin{array}{l} {F(x) = \dfrac{10890e^{0,1x}}{\left( {1 + 100e^{0,2x}} \right)^{\dfrac{3}{2}}}} \\ \left. \Rightarrow F'(x) = \dfrac{10890e^{0,1x}.0,1.\left( {1 + 100e^{0,2x}} \right)^{\dfrac{3}{2}} - \dfrac{3}{2}.\left( {1 + 100e^{0,2x}} \right)^{\dfrac{1}{2}}.100e^{0,2x}.0,2.10890e^{0,1x}}{\left( {1 + 100e^{0,2x}} \right)^{2}} \right. \\ {= \dfrac{10890e^{0,1x}.\left\lbrack {0,1 - 20e^{0,2x}} \right\rbrack}{\left( {1 + 100e^{0,2x}} \right)^{\dfrac{3}{2}}}} \\ \left. \Rightarrow F'(x) = 0,1 - 20e^{0,2x} = 0\Leftrightarrow x = 5\ln\dfrac{1}{200} \right. \\ \left. \Rightarrow F(x)_{\max} = F\left( {5\ln\dfrac{1}{200}} \right) \approx 419 \right. \end{array}$

Đáp số: 419

Đáp án cần điền là: 419

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.