Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc cuối HK1 lớp 10, 11, 12 tất cả các môn - Trạm số 2 - Ngày 27-28/12/2025 Xem chi tiết
Giỏ hàng của tôi
Trang chủ
Toán11

Một chiếc tàu lượn siêu tốc đang chuyển động theo phương thẳng đứng từ vị trí cao nhất

Một chiếc tàu lượn siêu tốc đang chuyển động theo phương thẳng đứng từ vị trí cao nhất xuống thấp nhất rồi lại đi lên. Biết rằng khoảng cách từ toa tàu đến mặt đất (tính bằng mét) theo thời gian t (giây) được cho bởi phương trình: $h(t) = 40 + 10\cos\left( \dfrac{\pi t}{3} \right),(t \geq 0)$

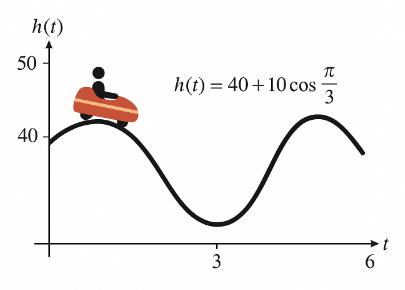
Trả lời cho các câu 1, 2, 3 dưới đây:

Câu hỏi số 1:
Thông hiểu

Tàu lượn ở gần mặt đất nhất vào thời điểm nào sau khi bắt đầu chuyển động?

Đáp án đúng là: A

Xem lời giải
Câu hỏi:811583
Phương pháp giải

Tìm GTNN của hàm $h(t)$ từ tính chất $\sin x \in \left\lbrack {- 1;1} \right\rbrack$ và $\cos x \in \left\lbrack {- 1,1} \right\rbrack$

Giải chi tiết

Tàu lượn ở gần mặt đất nhất khi $h(t)$ đạt GTNN

Ta có $h(t) = 40 + 10\cos\left( \dfrac{\pi t}{3} \right) \geq 40 - 10.1 = 30$ khi

$\left. \cos\left( {\dfrac{\pi}{3}t} \right) = - 1\Leftrightarrow\dfrac{\pi}{3}t = \dfrac{\pi}{2} + k\pi\Leftrightarrow t = 1,5 + 3k \right.$

Vậy thời điểm $t = 1,5$ giây thì tàu lượn gần mặt đất nhất

Đáp án cần chọn là: A

Câu hỏi số 2:
Thông hiểu

Thời điểm thứ 3 (theo giây) mà trong đó vận tốc của tàu lượn bằng 0 là:

Đáp án đúng là: D

Xem lời giải
Câu hỏi:811584
Phương pháp giải

Giải phương trình $h'(t) < 0$

Giải chi tiết

Vận tốc của tàu là $v(t) = h'(t) = - 10.\dfrac{\pi}{3}\sin\left( \dfrac{\pi t}{3} \right)$

Vận tốc bằng 0 khi $\left. \sin\left( \dfrac{\pi t}{3} \right) = 0\Leftrightarrow\dfrac{\pi t}{3} = k\pi\Leftrightarrow t = 3k \right.$

$\left. \Rightarrow t = 0;3;6;9;... \right.$ nên thời điểm thứ 3 mà vận tốc bằng 0 là $t = 9$

Đáp án cần chọn là: D

Câu hỏi số 3:
Vận dụng

Người thiết kế muốn hành trình của tàu lượn siêu tốc sao cho độ cao trung bình của tàu trong một chu kì dao động T (tức trong khoảng thời gian tàu đi hết một vòng lên – xuống – lên) là nhỏ nhất để giảm chi phí xây dựng đường ray. Hãy xác định tỉ số giữa độ cao trung bình trong một chu kì và độ cao cực đại của tàu.

Đáp án đúng là: C

Xem lời giải
Câu hỏi:811585
Phương pháp giải

Tìm chu kì của hàm lượng giác hàm $\cos\left( {at} \right)$ có chu kì $T = \dfrac{2\pi}{a}$

Áp dụng công thức tính độ cao trung bình trong khoảng thời gian T là $\overline{h} = \dfrac{1}{T}.{\int\limits_{0}^{T}{h(t)}}dt$

Giải chi tiết

$h(t) = 40 + 10\cos\left( \dfrac{\pi t}{3} \right),(t \geq 0)$ có chu kì $T = \dfrac{2\pi}{\dfrac{\pi}{3}} = 6$ giây

Khi đó chiều cao trung bình trong 1 chu kì là $\overline{h} = \dfrac{1}{6}{\int\limits_{0}^{6}\left\lbrack {40 + 10\cos\left( \dfrac{\pi t}{3} \right)} \right\rbrack}dt = 40$ (m)

Mà $h(t) = 40 + 10\cos\left( \dfrac{\pi t}{3} \right) \leq 40 + 10.1 = 50$ nên độ cao lớn nhất của tàu bằng 50 m

Vậy tỉ số cần tính là $\dfrac{40}{50} = \dfrac{4}{5}$

Đáp án cần chọn là: C

Quảng cáo

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn