Một chất điểm A chịu tác dụng của ba lực $\overset{\rightarrow}{F_{1}}$,
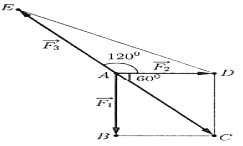
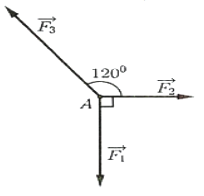
Một chất điểm A chịu tác dụng của ba lực $\overset{\rightarrow}{F_{1}}$, $\overset{\rightarrow}{F_{2}}$, $\overset{\rightarrow}{F_{3}}$ như hình vẽ biết chất điểm A đang ở trạng thái cân bằng. Tính độ lớn của các lực ${\overset{\rightarrow}{F}}_{2},{\overset{\rightarrow}{F}}_{3}$ biết rằng lực ${\overset{\rightarrow}{F}}_{1}$ có độ lớn 12 N.
Quảng cáo
Ta có vật ở trạng thái cân bằng nên ${\overset{\rightarrow}{F}}_{1} + {\overset{\rightarrow}{F}}_{2} + {\overset{\rightarrow}{F}}_{3} = \overset{\rightarrow}{0}$.
Tính $|\vec{F}_{2}|$: Tam giác tạo bởi $\vec{F}_{1}, \vec{F}_{2}$ và hợp lực của chúng là một tam giác vuông. Ta có: $|\vec{F}_{2}| = |\vec{F}_{1}| \cdot \tan(30^\circ)$
Tính $|\vec{F}_{3}|$: Độ lớn của $\vec{F}_{3}$ bằng độ lớn của hợp lực giữa $\vec{F}_{1}$ và $\vec{F}_{2}$. Áp dụng định lý Pytago: $|\vec{F}_{3}| = \sqrt{|\vec{F}_{1}|^2 + |\vec{F}_{2}|^2}$
Đặt ${\overset{\rightarrow}{F}}_{1} = \overset{\rightarrow}{AB},\overset{\rightarrow}{F_{2}} = \overset{\rightarrow}{AD},\overset{\rightarrow}{F_{3}} = \overset{\rightarrow}{AE}$. Vẽ hình chữ nhật ABCD.
Từ giả thiết: ${\overset{\rightarrow}{F}}_{1} + {\overset{\rightarrow}{F}}_{2} + {\overset{\rightarrow}{F}}_{3} = \overset{\rightarrow}{0}$ (vật ở trạng tháng cân bằng)
$\left. \Leftrightarrow\overset{\rightarrow}{AB} + \overset{\rightarrow}{AD} + \overset{\rightarrow}{AE} = \overset{\rightarrow}{0}\Leftrightarrow\overset{\rightarrow}{AC} = - \overset{\rightarrow}{AE}. \right.$
Ta có $\left. AB = 12,CAD = 180^{{^\circ}} - 120^{{^\circ}} = 60^{{^\circ}}\Rightarrow\angle BAC = 30^{{^\circ}} \right.$.
Tam giác ABC vuông tại $B$ nên: $BC = AB\tan 30^{{^\circ}} = 12 \cdot \dfrac{\sqrt{3}}{3} = 4\sqrt{3} = AD$;
Độ lớn lực ${\overset{\rightarrow}{F}}_{2}$ bằng $4\sqrt{3}N$
Suy ra $AC = \sqrt{AB^{2} + BC^{2}} = \sqrt{12^{2} + {(4\sqrt{3})}^{2}} = 8\sqrt{3}$.
Vậy $\left. \left| {\overset{\rightarrow}{F}}_{3} \right| = \middle| \overset{\rightarrow}{AE} \middle| = AC = 8\sqrt{3}N. \right.$
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
