Một chiếc đu quay có bán kính $75m$, tâm của vòng quay ở độ cao $90m$ so với mặt đất, thời
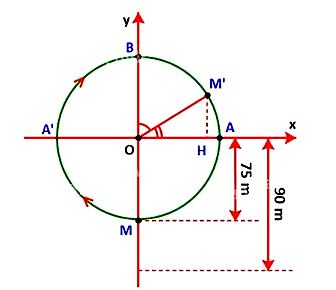
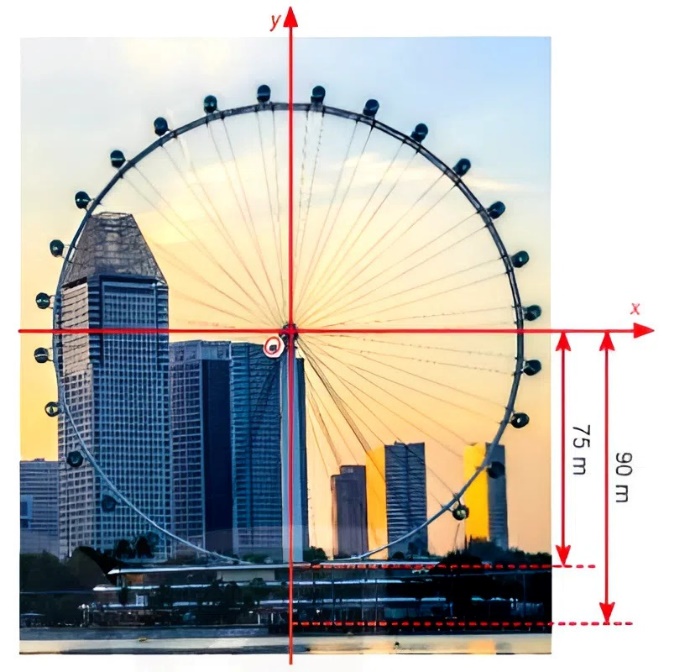
Một chiếc đu quay có bán kính $75m$, tâm của vòng quay ở độ cao $90m$ so với mặt đất, thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét so với mặt đất? (Làm tròn đến hàng đơn vị)
Đáp án đúng là:
Quảng cáo
Gắn bài toán vào đường tròn lượng giác có bán kính bằng 75m, gọi điểm sau khi cabin quay là $M'$ và $H$ là chân đường cao kẻ từ M xuống Ox. Khi đó tính góc $HOM'$ và độ dài $M'H$ từ đó tìm độ cao $M'$ so với mặt đất.
Do tính đối xứng, dù đu quay chuyển động theo chiều kim đồng hồ hay ngược chiều kim đồng hồ, ta đều thấy rằng độ cao của người đó là như nhau sau cùng một khoảng thời gian. Ở đây ta xét đu quay chuyển động theo chiều kim đồng hồ. Gắn đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m vào hệ trục tọa độ Oxy ta được hình bên:
Sau 20 phút quay cabin đi được một góc là $\dfrac{20}{30} \cdot 360^{{^\circ}} = 240^{{^\circ}}$ tức là đến vị trí điểm $M'$
Khi đó góc $\widehat{HOM^{\prime}} = 30^{{^\circ}}$ và $HM' = OM'.\sin 30^{{^\circ}} = 37,5(m)$.
Vậy sau 20 phút quay, người đó ở độ cao $37,5 + 90 = 127,5(~\text{m}) \approx 128m$.
Đáp án cần điền là: 128
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
