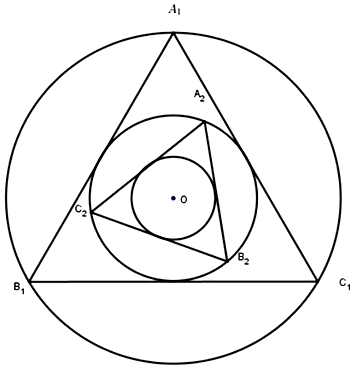
Cho một hình tròn tâm $O$ bán kính là $R = 60\text{m}$. Dựng tam

Câu hỏi số 819090:

Vận dụng

Cho một hình tròn tâm $O$ bán kính là $R = 60\text{m}$. Dựng tam giác đều $A_{1}B_{1}C_{1}$ nội tiếp đường tròn, sau đó lấy đường tròn nội tiếp tam giác $A_{1}B_{1}C_{1}$. Cứ tiếp tục làm quá trình như trên. Diện tích của tam giác $A_{9}B_{9}C_{9}$ là (kết quả làm tròn đến hàng phần mười)

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:819090

Phương pháp giải

Chứng minh các tam giác $A_{1}B_{1}C_{1},A_{2}B_{2}C_{2},\ldots$ có độ dài các cạnh tạo thành cấp số nhân với công bội $q_{c} = \dfrac{1}{2}$.

Nên diện tích các tam giác $A_{1}B_{1}C_{1},A_{2}B_{2}C_{2},\ldots$ là cấp số nhân với công bội $q_{S} = \dfrac{1}{4}$.

Từ $S_{1} = S_{A_{1}B_{1}C_{1}}$ tính $S_{9} = S_{A_{9}B_{9}C_{9}}$.

Giải chi tiết

Ta có $\left. R = 60\text{m}\Rightarrow OA_{1} = 60\text{m} \right.$

Xét $\text{Δ}A_{1}OB_{1}$ có $\left. A_{1}B_{1}~^{2} = 2OA_{1}~^{2} - 2OA^{2}~_{1} \cdot \text{cos}120^{0}\Rightarrow A_{1}B_{1}~^{2} = 2 \cdot 60^{2} + 2 \cdot 60^{2} \cdot \dfrac{1}{2} = 10800\text{m}^{2} \right.$

$\left. \Rightarrow A_{1}B_{1} = 60\sqrt{3}\text{m}^{2}\Rightarrow OA_{2} = 30\text{m} \right.$

Xét $~\Delta A_{2}OB_{2}$ có $\left. A_{2}B_{2}~^{2} = 2OA_{2}~^{2} - 2OA^{2}~_{2} \cdot \text{cos}120^{\circ}\Rightarrow A_{2}B_{2}~^{2} = 2.30^{2} + 2.30^{2} \cdot \dfrac{1}{2} = 2700\text{m}^{2} \right.$

$\left. \Rightarrow A_{2}B_{2} = 30\sqrt{3}\text{m}^{2} \right.$

Thực hiện tương tự, ta có các tam giác $A_{1}B_{1}C_{1},A_{2}B_{2}C_{2},\ldots$ có độ dài các cạnh tạo thành cấp số nhân với công bội $q_{c} = \dfrac{1}{2}$.

Nên diện tích các tam giác $A_{1}B_{1}C_{1},A_{2}B_{2}C_{2},\ldots$ là cấp số nhân với công bội $q_{S} = \dfrac{1}{4}$.

$S_{1} = S_{A_{1}B_{1}C_{1}} = \dfrac{A_{1}B_{1}~^{2} \cdot \sqrt{3}}{4} = \dfrac{10800\sqrt{3}}{4} = 2700\sqrt{3}\text{m}^{2}$.

$S_{9} = S_{1} \cdot \left( \dfrac{1}{4} \right)^{8} \approx 0,1m^{2}$.

Đáp án cần điền là: 0,1

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.