Để tránh núi, giao thông hiện tại phải đi vòng như mô hình trong hình. Để rút ngắn khoảng

Câu hỏi số 819490:

Vận dụng

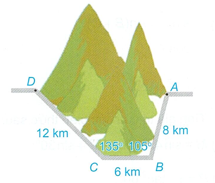
Để tránh núi, giao thông hiện tại phải đi vòng như mô hình trong hình. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ D tới A. Hỏi quãng đường đi thẳng từ D tới A dài bao nhiêu km (làm tròn đến hàng phần mười)?

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:819490

Phương pháp giải

Áp dụng định lí cosin trong tam giác ABC, tính AC: $AC^{2} = AB^{2} + BC^{2} - 2AB.BC.\cos B$.

Áp dụng định lí sin trong tam giác ABC, tính góc ACB $\dfrac{AB}{\sin C} = \dfrac{AC}{\sin B}$, suy ra góc ACD.

Áp dụng định lí cosin trong tam giác ACD, tính AD: $AD^{2} = AC^{2} + DC^{2} - 2AC.DC.\cos C$

Giải chi tiết

Áp dụng định lí cosin trong tam giác ABC ta có:

$AC = \sqrt{6^{2} + 8^{2} - 2.6.8 \cdot \cos 105^{{^\circ}}} \approx 11,2$ (km)

Lại có: Theo định lí $\sin$ thì

$\left. \dfrac{AB}{\sin C} = \dfrac{AC}{\sin B}\Rightarrow\sin\angle ACB = \dfrac{8 \cdot \sin 105^{{^\circ}}}{11,2} \right.$

$\left. \Rightarrow\widehat{ACB} \approx 43,6^{{^\circ}} \right.$

$\left. \Rightarrow\widehat{ACD} = 135^{{^\circ}} - 43,6^{{^\circ}} = 91,4^{{^\circ}} \right.$

Áp dụng định lí cosin trong tam giác ACD ta có:

$AD = \sqrt{12^{2} + 11,2^{2} - 2.12.11,2\cos 91,4^{{^\circ}}} \approx 16,6$ (km)

Đáp án cần điền là: 16,6

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10