Cho hình chóp S.ABCD có đáy là hình thang, $AD//BC,AD = xBC$. Gọi M, N
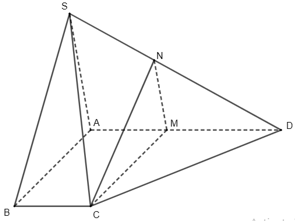
Cho hình chóp S.ABCD có đáy là hình thang, $AD//BC,AD = xBC$. Gọi M, N lần lượt là 2 điểm nằm trên AD, SD thỏa mãn $\dfrac{AM}{AD} = \dfrac{SN}{SD} = \dfrac{2}{5}$. Để $(CMN)//(SAB)$ thì khi đó giá trị của $x$ bằng bao nhiêu?
Đáp án đúng là:
Quảng cáo
Chứng minh $MN // SA$ dựa vào định lí Thales đảo và tỉ lệ đã cho. Suy ra $MN // (SAB)$.
Để $(CMN) // (SAB)$, cần thêm $CM // AB$.
$CM // AB \Leftrightarrow AMCB$ là hình bình hành $\Leftrightarrow AM = BC$.
Thay $AM = \dfrac{2}{5}AD$ và $BC = \dfrac{AD}{x}$ vào điều kiện $AM = BC$ để tìm $x$.
Để $(CMN)//(SAB)$, ta cần hai đường thẳng cắt nhau trong $(CMN)$ song song với $(SAB)$.
Vì $\dfrac{SN}{SD} = \dfrac{AM}{AD} = \dfrac{2}{5}$ (theo định lí Thales đảo trong $\triangle SAD$), suy ra $MN // SA$.
Mà $SA \subset (SAB)$, nên $MN // (SAB)$.
Để $(CMN)//(SAB)$, ta cần thêm $CM // AB$.
Vì ABCD là hình thang với $AD // BC$, để $CM // AB$ thì tứ giác $AMCB$ phải là hình bình hành
$\Leftrightarrow AM = BC$.
Lại có $AM = \dfrac{2}{5} AD$.
Để $AM = BC$ thì $BC = \dfrac{2}{5} AD$. Suy ra $AD =\dfrac{5}{2} BC$
Vậy giá trị của $x$ là $\dfrac{5}{2}=2,5$.
Đáp án cần điền là: 2,5
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
