Ông An dự định dùng xen kẽ 2 màu vàng, xanh để sơn trang trí một bức tường hình chữ nhật

Câu hỏi số 820397:

Vận dụng

Ông An dự định dùng xen kẽ 2 màu vàng, xanh để sơn trang trí một bức tường hình chữ nhật theo cách như sau: Đầu tiên dùng màu vàng sơn bức tường theo tấm bìa hình chữ nhật $H_{1}$ có chiều dài, chiều rộng tính theo đơn vị $m$ lần lượt là $\sqrt{5} + 1$ và 2 , sau đó cắt hình $H_{1}$ thành một hình vuông có cạnh bằng chiều rông của $H_{1}$ và hình chữ nhật $H_{2}$, rồi dùng màu xanh sơn tường theo hình $H_{2},\ldots$ cứ tiếp tục quá trình như vậy cho đến khi hình chữ nhật tạo ra có diện tích không đáng kể. Biết rằng tiền công để sơn mỗi mét vuông tường như vậy là 21 nghìn đồng. Hỏi ông An cần chuẩn bị tối đa bao nhiêu tiền công cho thợ sơn? (kết quả tính theo đơn vị nghìn đồng và làm tròn đến hàng nghìn).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:820397

Phương pháp giải

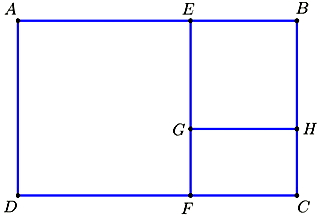
Tấm bìa ban đầu là hình chữ nhật $ABCD$ ký hiệu là $H_{1},H_{2}$ là hình chữ nhật $EBCF,H_{3}$ là hình chữ nhật $GHCF$…

Bài toán đưa về cấp số nhân với $\left( S_{(H_{n})} \right)$ là cấp số nhân lùi vô hạn có công bội $q = \dfrac{3 - \sqrt{5}}{2},S_{(H_{1})} = 2\left( {\sqrt{5} + 1} \right)$

Tổng diện tích là tổng cấp số nhân lùi vô hạn: $S = \dfrac{u_{1}}{1 - q}$

Giải chi tiết

Tấm bìa ban đầu là hình chữ nhật $ABCD$ ký hiệu là $H_{1},H_{2}$ là hình chữ nhật $EBCF,H_{3}$ là hình chữ nhật $GHCF$.

Hình chữ nhật $H_{n + 1}$ có được bằng cách cắt đi hình vuông có cạnh bằng chiều rộng của hình chữ nhật $H_{n}$.

Ta chứng minh 2 hình chữ nhật $H_{n},H_{n + 1}$ đồng dạng với tỷ số $\dfrac{1 + \sqrt{5}}{2}$, với mọi $n \in {\mathbb{N}}$.

Xét bài toán tổng quát: Cho hình chữ nhật $MNPQ$ có $\dfrac{MN}{NP} = \dfrac{1 + \sqrt{5}}{2}$. Gọi $I,J$ là các điểm lần lượt thuộc cạnh $MN,PQ$ sao cho tứ giác $MIJQ$ là hình vuông. Chứng minh rằng 2 hình chữ nhật $MNPQ$ và $NPJI$ là 2 hình chữ nhật đồng dạng.

Ta có 2 hình chữ nhật $MNPQ$ và $NPJI$ là 2 hình chữ nhật đồng dạng khi $\dfrac{MN}{NP} = \dfrac{NP}{PJ}$.

Vì $\left. \dfrac{MN}{NP} = \dfrac{1 + \sqrt{5}}{2}\Rightarrow MN = \dfrac{1 + \sqrt{5}}{2}NP\Rightarrow IN = \dfrac{\sqrt{5} - 1}{2}NP = JP\Rightarrow\dfrac{NP}{JP} = \dfrac{2}{\sqrt{5} - 1} = \dfrac{1 + \sqrt{5}}{2} \right.$.

Từ đó suy ra $\dfrac{MN}{NP} = \dfrac{NP}{PJ}$, do đó hai hình chữ nhật $MNPQ,NPJI$ đồng dạng với tỷ số $\dfrac{1 + \sqrt{5}}{2}$.

Theo kết quả này thì 2 hình chữ nhật $H_{n},H_{n + 1}$ đồng dạng với tỷ số $\dfrac{1 + \sqrt{5}}{2}$, với mọi $n \in {\mathbb{N}}$.

Gọi $S_{(H_{1})},S_{(H_{2})},S_{(H_{3})},\ldots$ là diện tích các hình chữ nhật $H_{1},H_{2},H_{3},\ldots$

Suy ra $\left( S_{(H_{n})} \right)$ là cấp số nhân lùi vô hạn có công bội $q = \dfrac{3 - \sqrt{5}}{2},S_{(H_{1})} = 2\left( {\sqrt{5} + 1} \right)$

Do đó tổng diện tích tường được sơn là:

$S = S_{(H_{1})} + S_{(H_{2})} + S_{(H_{3})} + \ldots + S_{(H_{n})} + \ldots = \dfrac{S_{(H_{1})}}{1 - q} = \dfrac{2\left( {\sqrt{5} + 1} \right)}{1 - \dfrac{3 - \sqrt{5}}{2}} = 6 + 2\sqrt{5}$.

Số tiền cần dùng là: $T = 21000.\left( {6 + 2\sqrt{5}} \right)$ đồng $\approx 220$ nghìn đồng

Kết quả làm tròn đến hàng nghìn nên số tiền tối đa ông An cần chuẩn bị là 220 nghìn đồng.

Đáp án cần điền là: 220

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.