Một cái bánh có dạng hình chóp, đáy là hình vuông

Câu hỏi số 821816:

Vận dụng

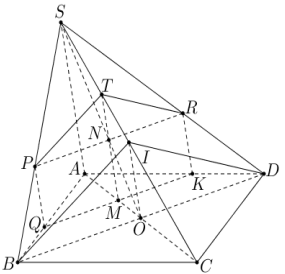
Một cái bánh có dạng hình chóp, đáy là hình vuông (minh họa như hình vẽ). Giả sử đình của bánh là S, đáy là hình vuông ABCD tâm O cạnh $5~\text{cm}$, $SB = SD$. Gọi M điểm tùy ý trên đoạn AO với $AM = x$, $(x > 0)$. Người ta cắt cái bánh bằng dao với mặt cắt là mặt phẳng $(\alpha)$ đi qua M, song song với SA và BD, $(\alpha)$ cắt SO, SB, AB lần lượt tại N, P, Q. Cho $SA = 5~\text{cm}$. Tìm $x$ để diện tích tứ giác MNPQ lớn nhất (kết quả cuối cùng làm tròn đến hàng phần chục).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:821816

Phương pháp giải

Xác định hình dạng của mặt cắt: Chứng minh rằng tứ giác MNPQ là hình chữ nhật bằng cách sử dụng các điều kiện song song đã cho và mối quan hệ giữa SA và BD.

Tính độ dài các cạnh của tứ giác: Sử dụng định lý Thales hoặc các tính chất hình học để biểu diễn độ dài MQ và MN theo $x$.

Lập hàm diện tích: Viết công thức tính diện tích tứ giác MNPQ theo $x$

Tìm giá trị lớn nhất: Sử dụng bất đẳng thức Cô-si để tìm giá trị của $x$ làm cho diện tích $S_{MNPQ}$ đạt giá trị lớn nhất.

Giải chi tiết

Ta có: $\left. SB = SD\Rightarrow \bigtriangleup SBC = \bigtriangleup SDC \right.$ (c.c.c) $\left. \Rightarrow\widehat{SCB} = \widehat{SCD} \right.$.

Gọi $I$ là trung điểm SC thì $\bigtriangleup IBC = \bigtriangleup IDC$ (c.g.c) $\left. \Rightarrow IB = ID \right.$.

Vậy $\bigtriangleup IBD$ cân tại $\left. I\Rightarrow IO\bot BD \right.$.

Mà $\left. OI//SA\Rightarrow SA\bot BD \right.$ (*)

Ta có: $\left\{ \begin{array}{l} {(\alpha)//BD} \\ {BD \subset (ABO)} \\ {(\alpha) \cap (ABO) = MQ} \end{array}\Rightarrow MQ//BD \right.$ (1)

Tương tự: $\left\{ \begin{array}{l} {(\alpha)//BD} \\ {BD \subset (SBO)} \\ {(\alpha) \cap (SBO) = NP} \end{array}\Rightarrow NP//BD \right.$ (2)

Từ (1) và (2) suy ra $MQ//NP//BD$ (3)

Ta có: $\left\{ \begin{array}{l} {(\alpha)//SA} \\ {SA \subset (SAO)} \\ {(\alpha) \cap (SAO) = MN} \end{array}\Rightarrow MN//SA \right.$ (4)

Tương tự: $\left\{ \begin{array}{l} {(\alpha)//SA} \\ {SA \subset (SAB)} \\ {(\alpha) \cap (SAB) = PQ} \end{array}\Rightarrow PQ//SA \right.$ (5)

Từ (4) và (5) suy ra $MN//PQ//SA$ (6)

Từ (3), (6) và (*) suy ra MNPQ là hình chữ nhật.

Ta có $S_{MNPQ} = MQ \cdot MN$.

Xét tam giác AQM ta có $\left. \widehat{A} = 45^{{^\circ}},\widehat{Q} = 45^{{^\circ}},\widehat{M} = 90^{{^\circ}}\Rightarrow \bigtriangleup AQM \right.$ cân tại M.

Vậy $MQ = AM = x$.

Xét tam giác SAO có $\left. MN//SA\Rightarrow\dfrac{MN}{SA} = \dfrac{OM}{OA} \right.$

$\left. \Rightarrow MN = SA \cdot \dfrac{OM}{OA} = 5 \cdot \dfrac{\dfrac{5\sqrt{2}}{2} - x}{\dfrac{5\sqrt{2}}{2}} = 5 - x\sqrt{2} \right.$

$\left. \Rightarrow S_{MNPQ} = MQ \cdot MN = x \cdot (5 - x\sqrt{2}) = \dfrac{1}{\sqrt{2}}x \cdot \sqrt{2}(5 - x\sqrt{2}) \right.$

Áp dụng bất đẳng thức Côsi cho hai số dương $x\sqrt{2}$ và $(5 - x\sqrt{2})$ :

$\left. x\sqrt{2}.(5 - x\sqrt{2}) \leq \left( \dfrac{x\sqrt{2} + 5 - x\sqrt{2}}{2} \right)^{2}\Leftrightarrow x\sqrt{2}.(5 - x\sqrt{2}) \leq \dfrac{5^{2}}{4}\Leftrightarrow S_{MNPQ} \leq \dfrac{25}{4\sqrt{2}} \right.$

Đẳng thức xảy ra khi: $\left. x\sqrt{2} = 5 - x\sqrt{2}\Leftrightarrow x = \dfrac{5\sqrt{2}}{4}\Leftrightarrow M \right.$ là trung điểm AO.

Vậy $x = \dfrac{5\sqrt{2}}{4} \approx 1,8~\text{cm}$ thì $S_{MNPQ}$ đạt giá trị lớn nhất.

Đáp án cần điền là: 1,8

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.