Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc ĐGNL/ĐGTD Tháng 12 ngày 13-14/12
 ↪ ĐGNL Hà Nội HSA (Trạm 2) ↪ ĐGNL HCM V-ACT (Trạm 2) ↪ ĐGTD Bách Khoa TSA (Trạm 4) ↪ ĐGNL SP Hà Nội SPT (Trạm 1)
Giỏ hàng của tôi
Trang chủ
Toán 10

Cho hình bình hành ABCD. Gọi M, N lần  lượt là trung điểm của DC, AB; P là giao điểm của AM,

Cho hình bình hành ABCD. Gọi M, N lần  lượt là trung điểm của DC, AB; P là giao điểm của AM, DB và Q là giao điểm của CN, DB.

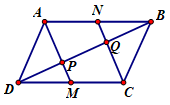
https://images.tuyensinh247.com/picture/2019/0605/17_2.PNG

Trả lời cho các câu 1, 2, 3, 4 dưới đây:

Câu hỏi số 1:
Thông hiểu

Có bao nhiêu vectơ khác \(\vec{0}\) có điểm đầu là B?

Đáp án đúng là: D

Xem lời giải
Câu hỏi:822767
Phương pháp giải

Khái niệm vectơ là đoạn thẳng có hướng, xác định các vectơ có điểm đầu là B.

Giải chi tiết

Các vectơ có điểm đầu là B: $\overset{\rightarrow}{BA},\overset{\rightarrow}{BN},\overset{\rightarrow}{BC},\overset{\rightarrow}{BD},\overset{\rightarrow}{BP},\overset{\rightarrow}{BQ}$.

Vậy có 6 vectơ.

Đáp án cần chọn là: D

Câu hỏi số 2:
Thông hiểu

Vectơ nào dưới đây cùng hướng với $\overset{\rightarrow}{DM}$

Đáp án đúng là: D

Xem lời giải
Câu hỏi:822768
Phương pháp giải

Hai vectơ được gọi là củng phương nếu chúng có giá song song hoặc trùng nhau.

Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngươc hướng.

Giải chi tiết

Vectơ cùng hướng với $\overset{\rightarrow}{DM}$ là $\overset{\rightarrow}{NB}$

Đáp án cần chọn là: D

Câu hỏi số 3:
Thông hiểu

Khẳng định nào dưới đây là đúng?

Đáp án đúng là: C

Xem lời giải
Câu hỏi:822769
Phương pháp giải

Xét từng đáp án, hai vectơ bằng nhau khi chúng cùng hướng và có độ dài bằng nhau.

Giải chi tiết

Ta có $\overset{\rightarrow}{CM}$ và $\overset{\rightarrow}{AN}$ là hai vectơ cùng phương, ngược hướng nên A sai.

$\overset{\rightarrow}{MD}$ và $\overset{\rightarrow}{BQ}$ là hai vectơ không cùng phương nên B sai.

$\overset{\rightarrow}{AM}$ và $\overset{\rightarrow}{NC}$ là hai vectơ cùng phương, cùng hướng.

Lại có $AM = NC = \dfrac{DC}{2}$

Vậy $\overset{\rightarrow}{AM} = \overset{\rightarrow}{NC}$

Đáp án cần chọn là: C

Câu hỏi số 4:
Thông hiểu

$\overset{\rightarrow}{PQ}$ bằng vectơ nào dưới đây?

Đáp án đúng là: A

Xem lời giải
Câu hỏi:822770
Phương pháp giải

Sử dụng tính chất đường trung bình của tam giác hoặc tỉ lệ đoạn thẳng để suy ra mối quan hệ giữa các đoạn thẳng $DP, PQ, QB$.

Giải chi tiết

Xét tam giác CDQ có M là trung điểm của DC và $MP//QC$ do đó P là trung điểm của DQ.

Tương tự xét tam giác ABP suy ra được Q là trung điểm của PB.

Vì vậy $DP = PQ = QB$ từ đó suy ra $\overset{\rightarrow}{DP}\ = \overset{\rightarrow}{PQ}\ = \overset{\rightarrow}{QB}$

Đáp án cần chọn là: A

Quảng cáo

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn