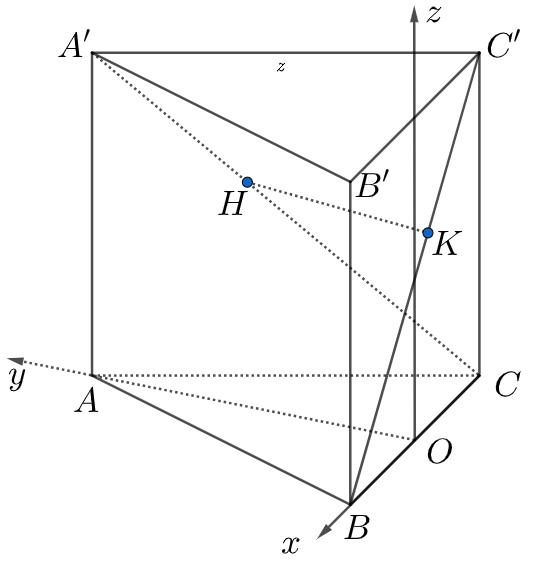
Điền số thích hợp vào chỗ trống.Một kiến trúc sư muốn xây dựng một tòa nhà biểu tượng
Điền số thích hợp vào chỗ trống.
Một kiến trúc sư muốn xây dựng một tòa nhà biểu tượng độc lạ cho thành phố. Trên bảng thiết kế tòa nhà có hình dạng là một khối lăng trụ tam giác đều, có cạnh bên $300$ mét và cạnh đáy và dài $200$ mét (tham khảo hình vẽ). Kiến trúc sư muốn xây dựng cây cầu hình $HK$ bắc xuyên tòa nhà ( điểm đầu thuộc cạnh $A'C,$ điểm cuối thuộc cạnh $BC'$) và cây cầu này sẽ được dát vàng với đơn giá 6 tỷ đồng trên 1 mét dài. Vì vậy để đáp ứng bài toán kinh tế, kiến trúc sư phải chọn vị trí cây cầu sao giá xây cây cầu là thấp nhất. Khi đó giá xây dựng cây cầu này hết ________ tỷ đồng. ( kết quả làm tròn đến hàng đơn vị )
Đáp án đúng là: 569
Quảng cáo
Gắn hệ trục toạ độ Oxyz và áp dụng công thức tính khoảng cách giữa hai đường thẳng chéo nhau $d\left( {A'C;BC'} \right) = \dfrac{\left| {\left\lbrack {\overset{\rightarrow}{a},\overset{\rightarrow}{b}} \right\rbrack.\overset{\rightarrow}{BC}} \right|}{\left| \left\lbrack {\overset{\rightarrow}{a},\overset{\rightarrow}{b}} \right\rbrack \right|}$
Chọn hệ trục $Oxyz$ như hình vẽ sau:
Gọi O là trung điểm cạnh $BC.$
$AO = 100\sqrt{3};OB = OC = 100$
Ta có: $O\left( {0;0;0} \right),A\left( {0;100\sqrt{3};0} \right);A'\left( {0;100\sqrt{3};300} \right),B\left( {100;0;0} \right),C\left( {- 100;0;0} \right),C'\left( {- 100;0;300} \right)$
Để tiền xây cầu thấp nhất thì cây cầu phải ngắn nhất. Tức là chiều dài cây cầu là khoảng cách giữa hai đường thẳng $A^{'}C$ và $BC^{'}.$
$\begin{array}{l} \left. \overset{\rightarrow}{A'C} = \left( {- 100; - 100\sqrt{3}; - 300} \right)\rightarrow\overset{\rightarrow}{a} = \left( {1;\sqrt{3};3} \right) \right. \\ \left. \overset{\rightarrow}{BC'} = \left( {- 200;0;300} \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \rightarrow\overset{\rightarrow}{b} = \left( {- 2;0;3} \right) \right. \\ {\overset{\rightarrow}{BC} = \left( {- 200;0;0} \right)} \end{array}$
$d\left( {A'C;BC'} \right) = \dfrac{\left| {\left\lbrack {\overset{\rightarrow}{a},\overset{\rightarrow}{b}} \right\rbrack.\overset{\rightarrow}{BC}} \right|}{\left| \left\lbrack {\overset{\rightarrow}{a},\overset{\rightarrow}{b}} \right\rbrack \right|} = \dfrac{\left| {\left( {3\sqrt{3}; - 9;2\sqrt{3}} \right).\left( {- 200;0;0} \right)} \right|}{\left| \left( {3\sqrt{3}; - 9;2\sqrt{3}} \right) \right|} = \dfrac{600\sqrt{3}}{2\sqrt{30}} = 30\sqrt{10}$
Vậy giá xây dựng cây cầu này là $30\sqrt{10}.6 = 180\sqrt{10} \approx 569$ tỷ đồng.
Đáp án cần điền là: 569
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
