Dựa vào thông tin dưới đây để trả lời các câu từ 75 đến 76 Bà Lan được tư vấn bổ
Dựa vào thông tin dưới đây để trả lời các câu từ 75 đến 76
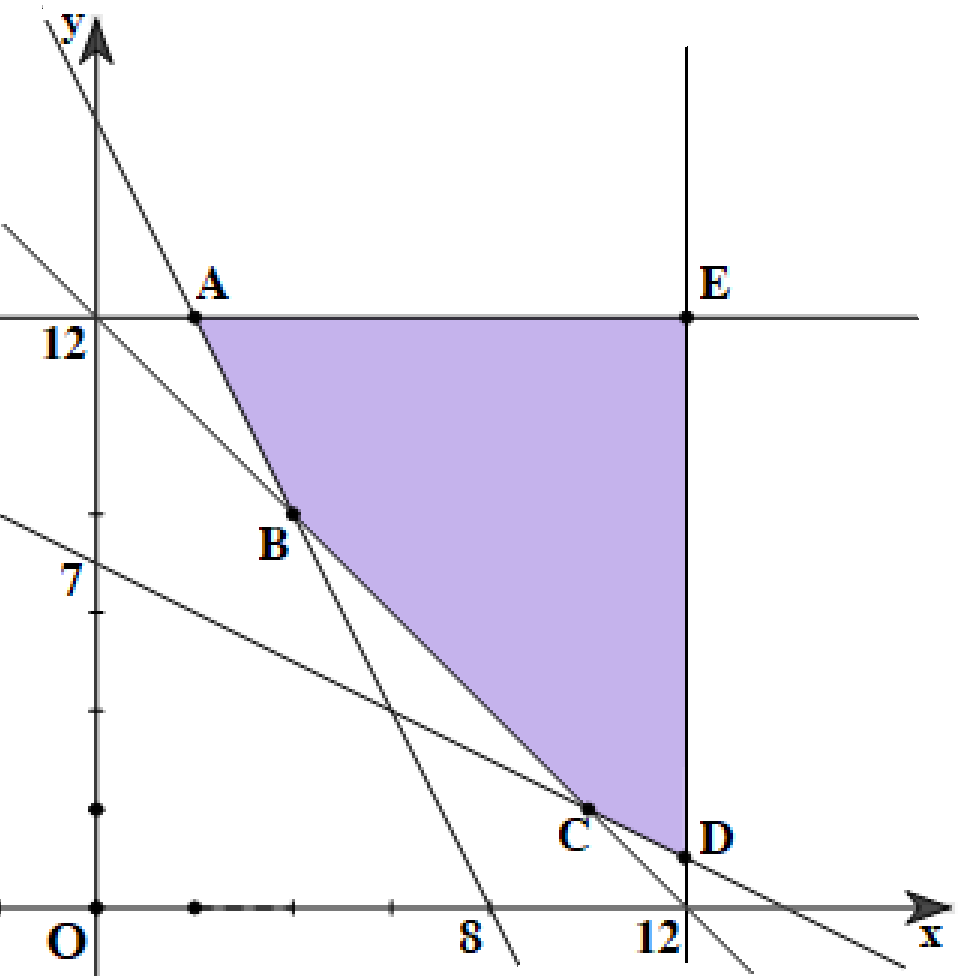
Bà Lan được tư vấn bổ sung chế độ ăn kiêng đặc biệt bằng cách sử dụng hai loại thực phẩm khác nhau là X và Y. Mỗi gói thực phẩm X chứa 20 đơn vị canxi, 20 đơn vị sắt và 10 đơn vị vitamin B. Mỗi gói thực phẩm Y chứa 20 đơn vị canxi, 10 đơn vị sắt và 20 đơn vị vitamin B. Yêu cầu hằng ngày tối thiểu trong chế độ ăn uống là 240 đơn vị canxi, 160 đơn vị sắt và 140 đơn vị vitamin B. Mỗi ngày không được dùng quá 12 gói mỗi loại. Biết 1 gói thực phẩm loại X giá 20000 đồng, 1 gói thực phẩm loại Y giá 25000 đồng. Gọi $x,y$ (gói) lần lượt là số gói thực phẩm loại X và loại Y mà bà Lan cần dùng mỗi ngày trong chế độ ăn kiêng để đáp ứng đủ nhu cầu cần thiết đối với canxi, sắt và vitamin B.
Trả lời cho các câu 1, 2 dưới đây:
Biểu thức biểu thị tổng chi phí mua các gói thực phẩm loại X và Y (đơn vị: nghìn đồng) của bà Lan là
Đáp án đúng là: B
Viết biểu thức đại số.
Đáp án cần chọn là: B
Bà Lan cần mua bao nhiêu gói thực phẩm loại X và loại Y để chi phí thấp nhất mà vẫn đảm bảo đáp ứng đủ nhu cầu cần thiết đối với canxi, sắt và vitamin B?
Đáp án đúng là: C
Tìm giá trị nhỏ nhất của biểu thức $F = ax + by$ trên miền đa giác (miền nghiệm của hệ bất phương trình bậc nhất hai ẩn $x,y$)
Biểu thức biểu thị tổng chi phí mua các gói thực phẩm loại X và Y (đơn vị: nghìn đồng) của bà Lan là:
$F = 20x + 25y$.
Hệ bất phương trình ràng buộc của bài toán:
$\left\{ \begin{array}{l} {0 \leq x \leq 12} \\ {0 \leq y \leq 12} \\ {20x + 20y \geq 240} \\ {20x + 10y \geq 160} \\ {10x + 20y \geq 140} \end{array} \right.(*)$
Biểu diễn miền nghiệm của (*) trên mặt phẳng tọa độ $Oxy$.
Miền nghiệm là ngũ giác $ABCDE$, trong đó: $A\left( {2;12} \right);B\left( {4;8} \right);C\left( {10;2} \right);D\left( {12;1} \right);E\left( {12;12} \right)$.
Giá trị của F tại các đỉnh của tứ giác như sau:
Tại $A\left( {2;12} \right)$: $F = 20.2 + 25.12 = 340$;
Tại $B\left( {4;8} \right)$: $F = 20.4 + 25.8 = 280$
Tại $C\left( {10;2} \right)$: $F = 20.10 + 25.2 = 250$;
Tại $D\left( {12;1} \right)$: $F = 20.12 + 25.1 = 265$.
Tại $E\left( {12;12} \right)$: $F = 20.12 + 20.12 = 540$.
Ta thấy F đạt giá trị nhỏ nhất là 250 tại $C\left( {10;2} \right)$.
Vậy chi phí tối thiểu phải trả là 250 nghìn đồng, khi bà Lan mua 10 gói thực phẩm loại X và 2 gói thực phẩm loại Y.
Đáp án cần chọn là: C
Quảng cáo
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
