Điều tra về chiều cao của học sinh khối lớp 10, ta có kết quả
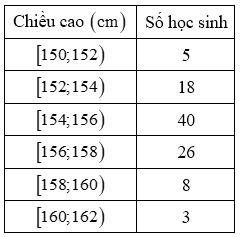
Điều tra về chiều cao của học sinh khối lớp 10, ta có kết quả sau:
| Đúng | Sai | |
|---|---|---|
| a) Tổng số học sinh điều tra bằng 100. | ||
| b) Chiều cao trung bình của các em học sinh trên là: 155,46. | ||
| c) Số trung vị của mẫu số liệu trên bằng 156,35 | ||
| d) Tứ phân vị thứ nhất của mẫu số liệu trên bằng 154,1 |
Đáp án đúng là: Đ; Đ; S; Đ
Quảng cáo
$n = m_{1} + \ldots + m_{k}$ là cỡ mẫu
$x_{i} = \dfrac{a_{i} + a_{i + 1}}{2}$ (với $i = 1,2,\ldots,k$ ) là giá trị đại diện của nhóm $\left\lbrack {a_{i};a_{i + 1}} \right)$.
Số trung bình của mẫu số liệu ghép nhóm kí hiệu là $\overline{x} = \dfrac{m_{1}x_{1} + \ldots + m_{k}x_{k}}{n}$
Để tính trung vị của mẫu số liệu ghép nhóm, ta làm như sau:
Bước 1: Xác định nhóm chứa trung vị. Giả sử đó là nhóm thứ $\text{p}:\left\lbrack {a_{p};a_{p + 1}} \right)$.
Bước 2: Trung vị là $M_{e} = a_{p} + \dfrac{\dfrac{n}{2} - \left( {m_{1} + \ldots + m_{p - 1}} \right)}{m_{p}} \cdot \left( {a_{p + 1} - a_{p}} \right)$
Để tính tứ phân vị thứ nhất $Q_{1}$ của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa $Q_{1}$, giả sử đó là nhóm thứ $\text{p}:\left\lbrack {a_{p};a_{p + 1}} \right)$. Khi đó $Q_{1} = a_{p} + \dfrac{\dfrac{n}{4} - \left( {m_{1} + \ldots + m_{p - 1}} \right)}{m_{p}} \cdot \left( {a_{p + 1} - a_{p}} \right)$
Đáp án cần chọn là: Đ; Đ; S; Đ
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
