Một chú thỏ ngày nào cũng ra bờ suối ở vị trí A, cách cửa hang của mình tại vị trí B là

Câu hỏi số 834150:

Vận dụng

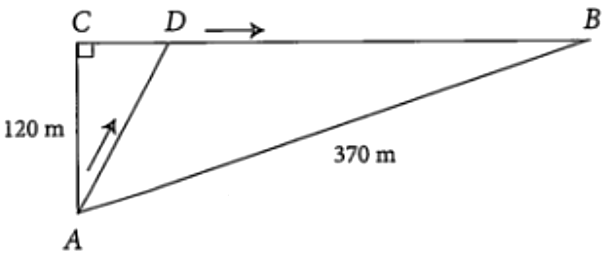
Một chú thỏ ngày nào cũng ra bờ suối ở vị trí A, cách cửa hang của mình tại vị trí B là 370m để uống nước, sau đó chú thỏ sẽ đến vị trí C cách vị trí A 120m để ăn cỏ rồi trở về hang. Tuy nhiên, hôm nay sau khi uống nước ở bờ suối, chú thỏ không đến vị trí C như mọi ngày mà chạy đến vị trí D để tìm cà rốt rồi mới trở về hang (xem hình bên dưới). Biết rằng, tổng thời gian chú thỏ chạy từ vị trí A đến vị trí D rồi về hang là 30 giây (không kể thời gian tìm cà rốt), trên đoạn AD chú thỏ chạy với vận tốc là $13~\text{m}/\text{s}$, trên đoạn BD chú thỏ chạy với vận tốc là $15~\text{m}/\text{s}$. Tính khoảng cách giữa hai vị trí C và D.

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:834150

Phương pháp giải

Đặt thời gian chạy trên AD là x, suy ra thời gian trên BD là $30 - x$. Tính AD và BD theo x.

Thiết lập phương trình: Tính BC, do $\bigtriangleup ACD$ vuông tại C và $CD = BC - BD$, ta có phương trình $\sqrt{{(13x)}^{2} - 120^{2}} = 350 - 15(30 - x)$.

Giải phương trình tìm x. Thay giá trị của x vào biểu thức của CD .

Giải chi tiết

Gọi thời gian chú thỏ chạy trên đoạn AD là $x(0 < x < 30)$(giây), khi đó thời gian chú thỏ chạy trên đoạn BD là $30 - x$ (giây).

Do đó, quãng đường AD và BD lần lượt là $13x(~\text{m})$ và $15(30 - x)(m)$.

Độ dài quãng đường BC là: $\sqrt{370^{2} - 120^{2}} = 350(~\text{m})$.

Tam giác ACD vuông tại C nên $CD = \sqrt{{(13x)}^{2} - 120^{2}}(~\text{m})$.

Mặt khác, $CD = BC - BD = 350 - 15(30 - x)(m)$.

Do đó, ta có: $\sqrt{{(13x)}^{2} - 120^{2}} = 350 - 15(30 - x)$.

Giải phương trình này và kết hợp với điều kiện $0 < x < 30$, ta nhận $x = 10$ (giây).

Vậy khoảng cách giữa vị trí C và vị trí D là: $350 - 15 \cdot (30 - 10) = 50(~\text{m})$.

Đáp án cần điền là: 50

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10