Lớp 12E có 20 bạn nam và 20 bạn nữ.
Lớp 12E có 20 bạn nam và 20 bạn nữ.
| Đúng | Sai | |
|---|---|---|
| a) Thầy quản nhiệm muốn chia lớp ra thành 4 tổ, mỗi tổ có 10 bạn thì có $C_{40}^{10}.C_{30}^{10}.C_{20}^{10}$ cách. | ||
| b) Xác suất để thầy quản nhiệm chia lớp ra thành 4 tổ, mỗi tổ có 10 bạn sao cho số lượng nam và nữ của mỗi tổ bằng nhau là 0,03. (Làm tròn đến hàng phần trăm) | ||
| c) Thầy quản nhiệm có thể chia lớp ra thành 4 tổ, mỗi tổ có 10 bạn sao cho số lượng các bạn nữ của các tổ lập thành một cấp số cộng và số lượng các bạn nam của mỗi tổ cũng vậy. | ||
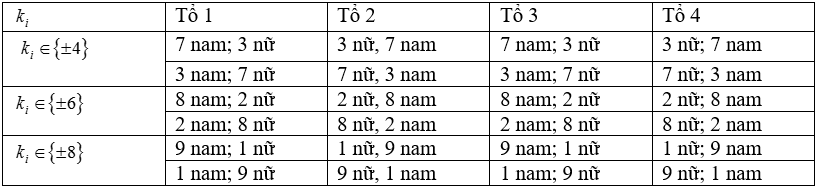
| d) Nghe lời thầy F có am hiểu về phong thủy, để cả lớp đạt NV1 trong kì thi quốc gia sắp tới thầy quản nhiệm chia lớp ra thành 4 tổ, mỗi tổ có 10 bạn sao cho tổ nào cũng có nam lẫn nữ và sự chênh lệch giữa số lượng nam và nữ trong tổ nhiều hơn 3 bạn. Nếu gọi $k_{1},k_{2},k_{3},k_{4}$ lần lượt là hiệu số giữa số lượng nam và nữ của tổ 1, 2, 3 và 4 thì $\left\{ {k_{1},k_{2},k_{3},k_{4}} \right\}$ lập thành một cấp số nhân với công bội $q \neq 1$. Xác suất để thầy quản nhiệm chia như vậy lớn hơn 0,0015. |
Đáp án đúng là: Đ; Đ; Đ; Đ
Quảng cáo
a) b) Sử dụng tổ hợp
c) Gọi số nữ ở 4 tổ là $n_{1},n_{2},n_{3},n_{4}$. Tổng $n_{1} + n_{2} + n_{3} + n_{4} = 20$.
Để lập thành cấp số cộng: $n_{1} + (n_{1} + d) + (n_{1} + 2d) + (n_{1} + 3d) = 20$.
d) Gọi số nam của tổ $i$ là $x_{i}$, số nữ là $10 - x_{i}$ ($0 < x_{i} < 10$).
Hiệu số giữa nam và nữ của tổ $i$ là: $k_{i} = x_{i} - (10 - x_{i}) = 2x_{i} - 10$.
a) Đúng: Chọn 10 bạn cho tổ 1: có $C_{40}^{10}$ cách.
Chọn 10 bạn cho tổ 2 từ 30 bạn còn lại: có $C_{30}^{10}$ cách.
Chọn 10 bạn cho tổ 3 từ 20 bạn còn lại: có $C_{20}^{10}$ cách.
10 bạn cuối cùng mặc định vào tổ 4: có $1$ cách.
Số cách chia lớp thành 4 tổ, mỗi tổ 10 bạn là $C_{40}^{10} \cdot C_{30}^{10} \cdot C_{20}^{10}$ cách.
b) Đúng: Số cách chia để mỗi tổ có 5 nam và 5 nữ:
Chia 20 nam vào 4 tổ (mỗi tổ 5 nam): $C_{20}^{5} \cdot C_{15}^{5} \cdot C_{10}^{5}$ cách.
Chia 20 nữ vào 4 tổ (mỗi tổ 5 nữ): $C_{20}^{5} \cdot C_{15}^{5} \cdot C_{10}^{5}$ cách.
Xác suất $P = \dfrac{{(C_{20}^{5} \cdot C_{15}^{5} \cdot C_{10}^{5})}^{2}}{C_{40}^{10} \cdot C_{30}^{10} \cdot C_{20}^{10}} \approx 0,0293$.
Làm tròn đến hàng phần trăm ta được 0,03.
c) Đúng: Có thể chia sao cho số lượng nữ và nam của các tổ lập thành cấp số cộng.
Gọi số nữ ở 4 tổ là $n_{1},n_{2},n_{3},n_{4}$. Tổng $n_{1} + n_{2} + n_{3} + n_{4} = 20$.
Để lập thành cấp số cộng:
$\begin{array}{l} {n_{1} + (n_{1} + d) + (n_{1} + 2d) + (n_{1} + 3d) = 20} \\ \left. \Rightarrow 4n_{1} + 6d = 20\Rightarrow 2n_{1} + 3d = 10 \right. \end{array}$.
Có các cặp $(n_{1},d)$ nguyên thỏa mãn như $\left. (2,2)\Rightarrow \right.$ số nữ là 2, 4, 6, 8.
Khi đó số nam tương ứng (để mỗi tổ có 10 người) sẽ là 8, 6, 4, 2 (cũng là một cấp số cộng với $d = - 2$).
d) Đúng: Gọi số nam của tổ $i$ là $x_{i}$, số nữ là $10 - x_{i}$ ($0 < x_{i} < 10$).
Hiệu số giữa nam và nữ của tổ $i$ là: $k_{i} = x_{i} - (10 - x_{i}) = 2x_{i} - 10$.
Theo đề bài: Tổ có cả nam lẫn nữ: $0 < x_{i} < 10$.
Sự chênh lệch $\left| k_{i} \middle| > 3 \right.$.
Vì $2x_{i}$ là số chẵn và 10 là số chẵn nên $k_{i}$ phải là số chẵn.
Suy ra $k_{i} \in \left\{ - 8, - 6, - 4,4,6,8 \right\}$.
Bộ số phải thỏa mãn đồng thời:
$\left\{ k_{1},k_{2},k_{3},k_{4} \right\}$ là CSN với công bội $q \neq 1$.
${\sum k_{i}} = {\sum{(x_{i} - m_{i})}} = {\sum x_{i}} - {\sum m_{i}} = 20 - 20 = 0$.
$k_{i} \in \left\{ - 8, - 6, - 4,4,6,8 \right\}$.
Từ đó ta thấy công bội chỉ có thể là $q = \pm 1$ vì nếu $q \neq \pm 1$ thì số hạng tăng rất nhanh.
Mà $\left. q \neq 1\Rightarrow q = - 1 \right.$
Ta xét các trường hợp của $k_{i} \in \left\{ - 8, - 6, - 4,4,6,8 \right\}$ như sau:
Số cách chọn để các tổ có 7 nam; 3 nữ hoặc 3 nam 7 nữ là:
$A = 2.C_{20}^{7}.C_{20}^{3}.C_{13}^{3}.C_{17}^{7}.C_{10}^{7}.C_{10}^{3}.C_{3}^{3}.C_{7}^{7}$
Số cách chọn để các tổ có 8 nam; 2 nữ hoặc 2 nam 8 nữ là:
$B = 2.C_{20}^{8}.C_{20}^{2}.C_{12}^{2}.C_{18}^{8}.C_{10}^{8}.C_{10}^{2}.C_{2}^{2}.C_{8}^{8}$
Số cách chọn để các tổ có 9 nam; 1 nữ hoặc 1 nam 9 nữ là:
$C = 2.C_{20}^{9}.C_{20}^{1}.C_{11}^{1}.C_{19}^{9}.C_{10}^{9}.C_{10}^{1}.C_{1}^{1}.C_{9}^{9}$
Xác suất cần tìm là: $\dfrac{A + B + C}{C_{40}^{10}.C_{30}^{10}.C_{20}^{10}} \approx 0,003 > 0,0015.$
Đáp án cần chọn là: Đ; Đ; Đ; Đ
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
