Trong không gian Oxyz cho trước với mặt nước phẳng lặng trùng với mặt phẳng (Oxy),
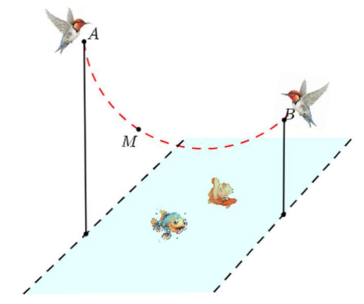
Trong không gian Oxyz cho trước với mặt nước phẳng lặng trùng với mặt phẳng (Oxy), đơn vị trên mỗi trục là mét; một chú chim bói cá đang đậu trên một cảnh cây ở vị trí $A(0; 0; 5)$ tiến hành bay xuống để thám thính ngang qua trên mặt hồ nước đến đậu trên một cảnh cây khác tại vị trí $B(4; 0; 4)$ theo quỹ đạo là một cung tròn hoàn hảo nằm trong mặt phẳng vuông góc với mặt nước đi qua điểm M thỏa mãn $\widehat{AMB} = 135^{o}$ (Điểm M như hình vẽ bên).
| Đúng | Sai | |
|---|---|---|
| a) Quỹ đạo bay của chim bói cá thuộc mặt phẳng $y = 0$. | ||
| b) Đường tròn chứa quỹ đạo bay của chim bói cá có tâm $I\left( {\dfrac{3}{2};0;\dfrac{5}{2}} \right)$. | ||
| c) Khoảng cách ngắn nhất mà chim bói cá bay xuống sát với mặt nước nhất là 3,58 m (làm tròn đến hàng phần trăm). | ||
| d) Biết rằng vận tốc của con chim bói cá là 2 m/s thì thời gian chim bói cá bay từ điểm $A(0; 0; 5)$ tới điểm gần mặt nước nhất mất 1,5 s (làm tròn đến hàng phần chục). |
Đáp án đúng là: Đ; S; Đ; Đ
Quảng cáo
Áp dụng biểu thức tọa độ các phép toán vecto trong không gian và kiến thức về đường tròn trong hình học phẳng.
a) Đúng: Hai điểm A, B cùng quỹ đạo bay đều thuộc mặt phẳng $y = 0$.
b) Sai: Vì quỹ đạo bay nằm trong mặt phẳng $y = 0$ nên tâm đường tròn chứa quỹ đạo là $I\left( {x_{I};0;z_{I}} \right)$.
Kẻ đường kính AC. Khi đó $\left. \widehat{AMC} = 90^{o}\Rightarrow\widehat{CMB} = \widehat{AMB} - \widehat{AMC} = 135^{o} - 90^{o} = 45^{o} \right.$.
Suy ra $\widehat{ACB} = \widehat{CMB} = 45^{o}$ (góc nội tiếp cùng chắn cung CB).
Mặt khác, tam giác IAB cân tại I có $\widehat{IAB} = 45^{o}$ nên tam giác IAB vuông cân tại I, hay $IA\bot IB$.
Hình biểu diễn trên mặt phẳng $y = 0$:
Ta có $\overset{\rightarrow}{IA} = ( - x_{I};0;5 - z_{I})$, $\overset{\rightarrow}{IB} = (4 - x_{I};0;4 - z_{I})$.
$IA\bot IB\Leftrightarrow\overset{\rightarrow}{IA}.\overset{\rightarrow}{IB} = 0$
$\Leftrightarrow - x_{I}\left( {4 - x_{I}} \right) + \left( {5 - z_{I}} \right)\left( {4 - z_{I}} \right) = 0$
$\Leftrightarrow - 4x_{I} + x_{I}{}^{2} + 20 - 9z_{I} + z_{I}{}^{2} = 0$ (*).
A, B thuộc quỹ đạo nên $\left. IA = IB\Leftrightarrow IA^{2} = IB^{2} \right.$
$\left. \Leftrightarrow\left( {0 - x_{I}} \right)^{2} + \left( {0 - 0} \right)^{2} + \left( {5 - z_{I}} \right)^{2} = \left( {4 - x_{I}} \right)^{2} + \left( {0 - 0} \right)^{2} + \left( {4 - z_{I}} \right)^{2} \right.$
$\left. \Leftrightarrow x_{I}{}^{2} + 25 - 10z_{I} + z_{I}{}^{2} = 16 - 8x_{I} + x_{I}{}^{2} + 16 - 8z_{I} + z_{I}{}^{2} \right.$
$\left. \Leftrightarrow 8x_{I} - 2z_{I} - 7 = 0\Leftrightarrow z_{I} = \dfrac{8x_{I} - 7}{2} \right.$.
Thay vào (*), ta được: $- 4x_{I} + x_{I}{}^{2} + 20 - 9.\dfrac{8x_{I} - 7}{2} + \left( \dfrac{8x_{I} - 7}{2} \right)^{2} = 0$
$\Leftrightarrow x_{I}{}^{2} - 4x_{I} + \dfrac{15}{4} = 0$$\Leftrightarrow\left\lbrack \begin{array}{l} {x_{I} = \dfrac{5}{2}} \\ {x_{I} = \dfrac{3}{2}} \end{array} \right.$.
Với $x_{I} = \dfrac{5}{2}$ thì $z_{I} = \dfrac{13}{2}$. Với $x_{I} = \dfrac{3}{2}$ thì $z_{I} = \dfrac{5}{2}$. Mà $z_{I} > z_{A}$ nên $I\left( {\dfrac{5}{2};0;\dfrac{13}{2}} \right)$.
c) Đúng: Bán kính quỹ đạo là $R = IA = \sqrt{\left( {0 - \dfrac{5}{2}} \right)^{2} + \left( {0 - 0} \right)^{2} + \left( {5 - \dfrac{13}{2}} \right)^{2}} = \dfrac{\sqrt{34}}{2}$ (m).
Khoảng cách ngắn nhất giữa chim bói cá và mặt nước là $z_{I} - R = \dfrac{13}{2} - \dfrac{\sqrt{34}}{2} \approx 3,58$ (m).
d) Đúng: Gọi H là điểm mà chim bói cá sát với mặt nước nhất.
Khi đó một vecto chỉ phương của IH là $\overset{\rightarrow}{u_{IH}} = \left( {0;0; - 1} \right)$, $\overset{\rightarrow}{IA} = \left( {- \dfrac{5}{2};0; - \dfrac{3}{2}} \right)$.
$\cos\left( {\overset{\rightarrow}{IA},\overset{\rightarrow}{IH}} \right) = \dfrac{\overset{\rightarrow}{IA}.\overset{\rightarrow}{IH}}{IA.IH} = \dfrac{0.\left( {- \dfrac{5}{2}} \right) + 0.0 - 1.\left( {- \dfrac{3}{2}} \right)}{\sqrt{0^{2} + 0^{2} + {( - 1)}^{2}}.\sqrt{\left( {- \dfrac{5}{2}} \right)^{2} + 0^{2} + \left( {- \dfrac{3}{2}} \right)^{2}}} = \dfrac{3\sqrt{34}}{34}$.
$\left. \Rightarrow\left( {\overset{\rightarrow}{IA},\overset{\rightarrow}{IH}} \right) \approx 1,03 \right.$ (rad).
Độ dài cung nhỏ AH là $l_{AH} \approx 1,03.\dfrac{\sqrt{34}}{2} \approx 3$ (m).
Vậy thời gian chim bói cá bay từ A đến H là xấp xỉ $\dfrac{3}{2} = 1,5$ (s).
Đáp án cần chọn là: Đ; S; Đ; Đ
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
