Anh Nghĩa có một khu đất hình thang vuông ABCD với $AB = 100 m$, $DC = 60 m$ và $AD

Câu hỏi số 855039:

Vận dụng

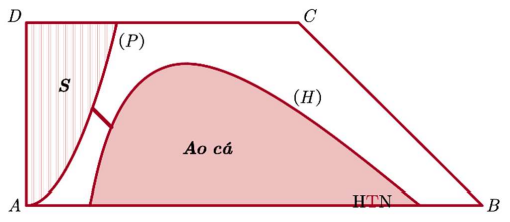
Anh Nghĩa có một khu đất hình thang vuông ABCD với $AB = 100 m$, $DC = 60 m$ và $AD = 40 m.$ Anh ấy đã đào một cái hồ để nuôi cá, hồ được bao bởi cạnh AB và một phần của đường cong $(\mathcal{H}),$ biết rằng $(\mathcal{H})$ chứa các điểm K sao cho tích khoảng cách từ K đến AD và BC luôn bằng $600\sqrt{2}m.$ Anh Nghĩa xây thêm một nhà kho để chứa thức ăn cho cá được tạo bởi cạnh AD, DC và đường cong Parabol $(P)$ có đỉnh A, biết rằng phần đất để xây nhà kho có diện tích $S = \dfrac{1600}{3}$ $\left( m^{2} \right).$ Anh Nghĩa suy nghĩ và muốn xây một con đường thẳng đi từ nhà kho đến ao cá để vận chuyển thức ăn cho cá. Hãy tính độ dài con đường ngắn nhất? (Đơn vị: mét, làm tròn đến hàng phần trăm).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:855039

Phương pháp giải

Tìm phương trình của (P) và (H). Giả sử M thuộc (P), N thuộc (H) sao cho MN ngắn nhất, khi đó tiếp tuyến của (P), (H) tại M, N song song với nhau. Từ đó tính MN.

Giải chi tiết

Gắn hệ trục tọa độ Oxy sao cho O trùng A, B thuộc tia Ox, D thuộc tia Oy.

Khi đó $A(0; 0)$, $B(100; 0)$, $C(60; 40)$, $D(0; 40)$.

Từ tọa độ hai điểm B, C, ta tìm được phương trình đường thẳng BC: $x + y – 100 = 0$.

Giả sử $K(x; y)$. Ta có

$\left. d\left( {K,AD} \right).d\left( {K,BC} \right) = 600\sqrt{2}\Leftrightarrow x.\dfrac{\left| {x + y - 100} \right|}{\sqrt{1^{2} + 1^{2}}} = 600\sqrt{2} \right.$

$\left. \Leftrightarrow\left\lbrack \begin{array}{l} {x + y - 100 = \dfrac{1200}{x}} \\ {x + y - 100 = \dfrac{- 1200}{x}} \end{array} \right.\Leftrightarrow\left\lbrack \begin{array}{l} {y = - x + 100 + \dfrac{1200}{x}} \\ {y = - x + 100 - \dfrac{1200}{x}} \end{array} \right. \right.$

Vì đồ thị $(H)$ có điểm cực trị nên $(H)$: $- x + 100 - \dfrac{1200}{x}$.

Giả sử (P): $y = ax^{2}$. Xét $\left. y = ax^{2} = 40\Leftrightarrow x = \sqrt{\dfrac{40}{a}} \right.$.

Ta có $S = {\int\limits_{0}^{\sqrt{\frac{40}{a}}}{\left( {40 - ax^{2}} \right)dx}} = \dfrac{1600}{3}$

$\Leftrightarrow 40\sqrt{\dfrac{40}{a}} - \dfrac{a}{3}\left( \sqrt{\dfrac{40}{a}} \right)^{3} - \dfrac{1600}{3} = 0\Leftrightarrow a = \dfrac{1}{10}$.

Vậy (P): $y = \dfrac{1}{10}x^{2}$.

Giả sử M thuộc $(P)$, N thuộc $(H)$ sao cho MN ngắn nhất.

Ta có $M\left( {m;\dfrac{m^{2}}{10}} \right)$, $N\left( {n; - n + 100 - \dfrac{1200}{n}} \right)$.

Để MN ngắn nhất thì tiếp tuyến của $(P)$, $(H)$ tại M, N song song với nhau

$\left. \Leftrightarrow k_{M} = k_{N}\Leftrightarrow y'_{M} = y'_{N}\Leftrightarrow\dfrac{m}{5} = - 1 + \dfrac{1200}{n^{2}}\Leftrightarrow m = \dfrac{6000}{n^{2}} - 5 \right.$.

Suy ra $M\left( {\dfrac{6000}{n^{2}} - 5;\dfrac{1}{10}\left( {\dfrac{6000}{n^{2}} - 5} \right)^{2}} \right)$.

$MN^{2} = \left( {\dfrac{6000}{n^{2}} - 5 - n} \right)^{2} + \left\lbrack {\dfrac{1}{10}\left( {\dfrac{6000}{n^{2}} - 5} \right)^{2} + n - 100 + \dfrac{1200}{n}} \right\rbrack^{2}$

$ = f(n)$.

$f'(n) = 0\Leftrightarrow n \approx 18,13 \right.$, khi đó $MN \approx 5,23$.

Đáp án cần điền là: 5,23

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.