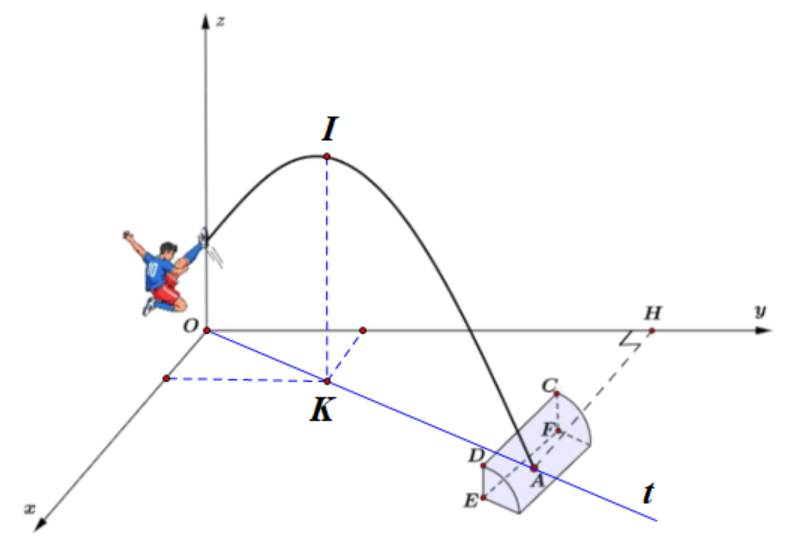
Trong trận đấu giữa Thụy Điển và Anh tại giải vô địch bóng đá thế

Câu hỏi số 855041:

Vận dụng

Trong trận đấu giữa Thụy Điển và Anh tại giải vô địch bóng đá thế giới, khi thời gian trận đấu sắp kết thúc, Zlatan Ibrahimović đã thực hiện một cú xe đạp chổng ngược móc bóng từ khoảng cách xa vào lưới đội tuyển Anh. Đây được coi là một trong những bàn thắng đẹp nhất lịch sử bóng đá thế giới với khoảng cách xa nhất từng được ghi bằng kỹ thuật này. Chọn hệ trục tọa độ Oxyz (đơn vị trên mỗi trục tính theo mét) sao cho $(Oxy)$ trùng với mặt đất, tại thời điểm Ibra tung người móc bóng quả bóng thuộc tia Oz và có độ cao 2m, bay theo quỹ đạo của một Parabol thuộc mặt phẳng vuông góc với mặt đất rơi xuống đất tại vị trí điểm A nằm trong khung thành. Biết $d(A,Oy) = AH = 8$ $(H \in Oy)$ và $OH = 15$. Sau khi bay lên không trung quả bóng đạt độ cao lớn nhất tại điểm có hoành độ $x = 3$. Tại thời điểm bóng bắt đầu bay vào khung thành (tức là bóng nằm trên vạch kẻ ngang của khung thành) thì độ cao của quả bóng so với mặt đất là bao nhiêu mét? Biết rằng khung thành CDEF nằm trong mặt phẳng vuông góc với mặt đất và đi qua 2 điểm $M(4; 15; -2)$, $N(8; 14; 6)$. (Làm tròn kết quả đến hàng phần trăm).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:855041

Phương pháp giải

Áp dụng biểu thức tọa độ các phép toán vectơ.

Giải chi tiết

Gọi các điểm như hình vẽ.

Ta có: $O(0; 0; 0)$, $A(8; 15; 0)$, $B(0; 0; 2)$.

$\overset{\rightarrow}{OA} = (8;15;0)$, $\left. \overset{\rightarrow}{OB} = (0;0;2)\Rightarrow\left\lbrack {\overset{\rightarrow}{OA},\overset{\rightarrow}{OB}} \right\rbrack = (30; - 16;0) = 2(15; - 8;0) \right.$.

Phương trình mặt phẳng (OAB) đi qua $O(0; 0; 0)$ và có vectơ pháp tuyến $\overset{\rightarrow}{n} = (15; - 8;0)$:

$15x - 8y = 0$.

$\overset{\rightarrow}{MN} = (4; - 1;8)$, $\overset{\rightarrow}{k} = (0;0;1)$ $\Rightarrow$ $\left\lbrack {\overset{\rightarrow}{MN},\overset{\rightarrow}{k}} \right\rbrack = ( - 1; - 4;0) = - (1;4;0)$.

Mặt phẳng $(CDEF)$ đi qua $M(4; 15; -2)$ và có vectơ pháp tuyến $\overset{\rightarrow}{n} = (1;4;0)$ nên có phương trình:

$\left. 1(x - 4) + 4(y - 15) = 0\Leftrightarrow x + 4y - 64 = 0 \right.$.

Xét hệ trục $Otz$. Gọi parabol $(P)$: $z = at^{2} + bt + c$.

$\left. B(0;2) \in (P)\Rightarrow c = 2 \right.$ (1)

$\left. OA = \sqrt{8^{2} + 15^{2} + 0^{2}} = 17\Rightarrow A(17;0) \in (P)\Rightarrow 289a + 17b + c = 0 \right.$ (2)

Ta có $\left. I \in (OAB)\Rightarrow 15.3 - 8y_{I} = 0\Leftrightarrow y_{I} = \dfrac{45}{8} = y_{K} \right.$.

$\left. OK = \sqrt{3^{2} + \left( \dfrac{45}{8} \right)^{2}} = \dfrac{51}{8}\Rightarrow t_{K} = t_{I} = \dfrac{51}{8} \right.$.

I là điểm cực trị của $(P)$ nên $\left. z'\left( t_{I} \right) = 0\Leftrightarrow 2at_{I} + b = 0\Leftrightarrow \dfrac{51}{4}a + b = 0 \right.$ (3)

Từ (1), (2) và (3) suy ra $a = - \dfrac{8}{289}$, $b = \dfrac{6}{17}$, $c = 2$

$\Rightarrow(P):z = - \dfrac{8}{289}t^{2} + \dfrac{6}{17}t + 2$.

Đường thẳng OA đi qua $O(0; 0; 0)$ và có vectơ chỉ phương $\left. \overset{\rightarrow}{u} = \overset{\rightarrow}{OA} = (8;15;0)\Rightarrow OA:\left\{ \begin{array}{l} {x = 8t} \\ {y = 15t} \\ {z = 0} \end{array} \right. \right.$.

Gọi G là giao điểm của OA và mặt phẳng (CDEF).

Ta có $\left. G \in OA\Rightarrow G(8t;15t;0) \in (CDEF):x + 4y - 64 = 0 \right.$.

$\left. \Rightarrow 8t + 4.15t - 64 = 0\Leftrightarrow t = \dfrac{16}{17} \right.$.

Xét trong mặt phẳng Otz: $\left. OG = \sqrt{{(8t)}^{2} + {(15t)}^{2} + 0^{2}} = 17t = 17.\dfrac{16}{17} = 16\Rightarrow G(16;0) \right.$.

Suy ra độ cao của quả bóng lúc vào khung thành là $z = - \dfrac{8}{289}.16^{2} + \dfrac{6}{17}.16 + 2 = \dfrac{162}{289} \approx 0,56$ (m).

Đáp án cần điền là: 0,56

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.