Một trang trại dự định dành 100 ha đất để trồng ba loại cây: Cao su, Cà

Câu hỏi số 855626:

Vận dụng

Một trang trại dự định dành 100 ha đất để trồng ba loại cây: Cao su, Cà phê và Hồ tiêu. Lợi nhuận hàng năm ước tính của Cao su là 40 triệu đồng/ha, Cà phê là 60 triệu đồng/ha và Hồ tiêu là 80 triệu đồng/ha. Do các yếu tố về quy hoạch và tài nguyên nước, diện tích trồng các loại cây phải tuân thủ các điều kiện sau:

1. Tổng diện tích trồng Cà phê và Hồ tiêu không được vượt quá diện tích trồng Cao su.

2. Diện tích trồng Hồ tiêu không được vượt quá 20 ha.

3. Diện tích trồng Cà phê không được vượt quá 3 lần diện tích trồng Hồ tiêu.

Tổng lợi nhuận thu được hàng năm của trang trại đó lớn nhất là bao nhiêu tỷ đồng?

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:855626

Phương pháp giải

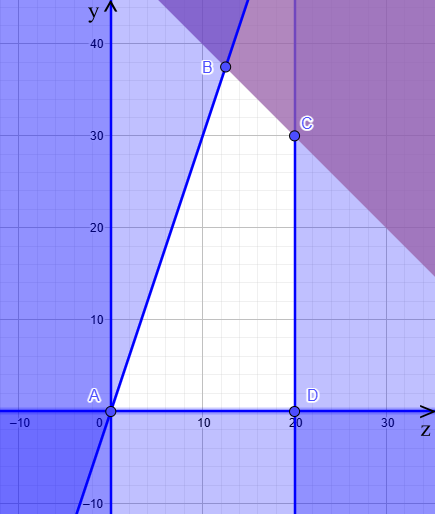
Thiết lập hệ bất phương trình dựa trên các điều kiện ràng buộc của đề bài.

Biểu diễn hàm mục tiêu (tổng lợi nhuận).

Xét các đỉnh của miền nghiệm để tìm giá trị lớn nhất của hàm mục tiêu.

Giải chi tiết

Gọi diện tích trồng Cao su, Cà phê, Hồ tiêu lần lượt là x, y, z (đơn vị: ha), $0 \leq x,y,z \leq 100$.

Tổng diện tích: $\left. x + y + z = 100\Rightarrow x = 100 - y - z \right.$.

Theo đề bài ta có:

1. Tổng diện tích trồng Cà phê và Hồ tiêu không được vượt quá diện tích trồng Cao su.

$\left. y + z \leq x\Rightarrow x - y - z \geq 0 \right.$

2. Diện tích trồng Hồ tiêu không được vượt quá 20 ha: $\left. z \leq 20\Rightarrow - z + 20 \geq 0 \right.$

3. Diện tích trồng Cà phê không được vượt quá 3 lần diện tích trồng Hồ tiêu:

$\left. y \leq 3z\Rightarrow - y + 3z \geq 0 \right.$

Hệ phương trình: $\left\{ \begin{array}{l} {0 \leq x,y,z \leq 100} \\ {x - y - z \geq 0} \\ {- z + 20 \geq 0} \\ {- y + 3z \geq 0} \end{array} \right.$

Tổng lợi nhuận tính theo đơn vị triệu đồng: $T = 40x + 60y + 80z$

Thay $x = 100 - y - z$ vào biểu thức T:

$T = 40(100 - y - z) + 60y + 80z = 4000 - 40y - 40z + 60y + 80z$

$\left. \Rightarrow T = 4000 + 20y + 40z \right.$

Thay $x = 100 - y - z$ vào HPT, có

$\left. \left\{ \begin{array}{l} {100 - y - z - y - z \geq 0} \\ {- z + 20 \geq 0} \\ {- y + 3z \geq 0} \end{array} \right.\Leftrightarrow\left\{ \begin{array}{l} {y + z \leq 50} \\ {z \leq 20} \\ {y \leq 3z} \\ {y,z \geq 0} \end{array} \right. \right.$

Biểu diễn miền nghiệm trên hệ trục tọa độ Ozy (với trục nằm ngang là Oz, trục thẳng đứng là Oy):

Miền nghiệm là tứ giác ABCD với các đỉnh: $A(0;0)$, $B(12,5;37,5)$, $C(20;30)$, $D(20;0)$

Ta có $T(0;0) = 4000$; $T(20;0) = 4800$; $T(20;30) = 5400$; $T(12,5;37,5) = 5250$

Giá trị $T_{max} = 5400$ triệu đồng = 5,4 tỷ đồng đạt được tại $C(20;30)$.

Đáp án cần điền là: 5,4

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.