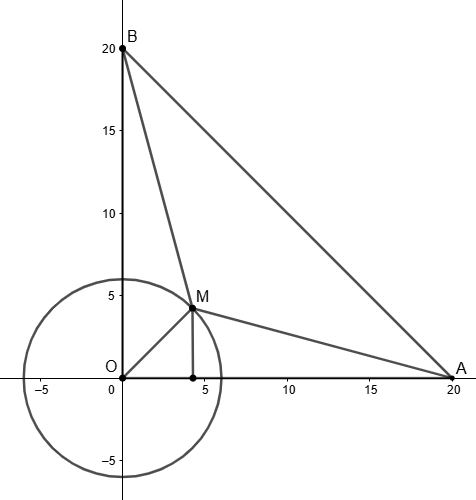
Mặt cầu tâm I bán kính $R > 0$ là tập hợp tất cả các điểm trong không gian cách I một

Câu hỏi số 855627:

Vận dụng

Mặt cầu tâm I bán kính $R > 0$ là tập hợp tất cả các điểm trong không gian cách I một khoảng bằng R. Trong không gian với hệ tọa độ Oxyz, đơn vị trên hệ trục là cemtimet, một tổ kiến có bề mặt là một mặt cầu tâm là gốc tọa độ và bán kính $R = 6~\text{cm}$, ở điểm $A(20;0;0)$ có 10 miếng mồi và ở điểm $B(0;20;0)$ có 3 miếng mồi. Một con kiến trên bề mặt tổ, mỗi lần đi đến A hoặc B tha đúng một miếng mồi về tổ. Hỏi tổng quãng đường ngắn nhất con kiến đó đi là bao nhiêu centimet để con kiến tha hết 13 miếng mồi về tổ (kết quả làm tròn hàng đơn vị)?

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:855627

Phương pháp giải

Xác định khoảng cách ngắn nhất từ tổ đến mồi: Tính khoảng cách từ bề mặt mặt cầu đến các điểm A và B: $d = OA - R = OB - R = 14$ cm.

Để quãng đường ngắn nhất, kiến sẽ lấy hết mồi ở A (10 lần) rồi mới chuyển sang B (3 lần). Lộ trình gồm các chuyến đi-về khép kín tại điểm gần mồi nhất, chỉ duy nhất một lần chuyển tiếp giữa hai khu vực.

Tìm điểm M trên mặt cầu sao cho tổng khoảng cách AM + MB là nhỏ nhất .

Tính tổng quãng đường = Quãng đường 12 chuyến đi - về cơ bản + Quãng đường chuyến chuyển tiếp $\left. A\rightarrow M\rightarrow B \right.$.

Giải chi tiết

Tổ kiến là mặt cầu $(S)$ tâm $O(0,0,0)$, bán kính $R = 6$ cm.

Điểm đặt mồi: $A(20,0,0)$ và $B(0,20,0)$.

Khoảng cách từ tâm O đến các điểm mồi: $OA = 20$ cm, $OB = 20$ cm.

Khoảng cách ngắn nhất từ một điểm trên bề mặt tổ đến điểm mồi:

$d_{min}(S,A) = OA - R = 20 - 6 = 14$ cm.

$d_{min}(S,B) = OB - R = 20 - 6 = 14$ cm.

Xác định lộ trình tối ưu:

Con kiến cần thực hiện 13 chuyến đi (10 chuyến đến A và 3 chuyến đến B). Để tổng quãng đường là ngắn nhất, con kiến nên lấy hết mồi ở một điểm rồi mới chuyển sang điểm kia để giảm thiểu số lần di chuyển giữa hai hướng A và B.

Giả sử kiến lấy 10 miếng ở A trước, sau đó lấy 3 miếng ở B.

Lộ trình gồm 26 đoạn (13 lượt đi và 13 lượt về):

- Chuyến 1 đến 9 (tại A): Kiến đi từ bề mặt tổ đến A và quay lại điểm gần A nhất trên tổ ($M_{A}$).

Quãng đường: 14 (lượt đi đầu) $+ 9.(14 + 14)$ (9 chuyến khép kín) $= 14 + 252 = 266$ cm.

- Chuyến chuyển tiếp (từ A sang B): Kiến lấy miếng mồi cuối cùng ở A, nhưng thay vì quay về $M_{A}$, nó sẽ quay về một điểm M trên mặt cầu sao cho tổng khoảng cách đến A và B là nhỏ nhất để chuẩn bị cho chuyến đi tiếp theo đến B.

Quãng đường: $d(A,M) + d(M,B)$.

- Chuyến 11 đến 13 (tại B): Sau khi từ B về tổ, kiến thực hiện nốt các chuyến còn lại tại B và kết thúc tại điểm gần B nhất trên tổ ($M_{B}$).

Quãng đường: $2.(14 + 14)$ (2 chuyến khép kín) $+ 14$ (lượt về cuối) $= 56 + 14 = 70$.

Tìm $M \in (S)$ để $f(M) = d(A,M) + d(M,B)$ đạt giá trị nhỏ nhất.

M nằm trên mặt phẳng $x = y$, $z = 0$. Với $R = 6$, $M$ có tọa độ $(3\sqrt{2},3\sqrt{2},0)$.

$d(A,M) = \sqrt{\left( {20 - 3\sqrt{2}} \right)^{2} + \left( {3\sqrt{2}} \right)^{2}} = \sqrt{436 - 120\sqrt{2}} \approx 16,32$ cm.

$d(B,M) = d(A,M) \approx 16,32$ cm.

$\left. \Rightarrow d(A,M) + d(M,B) \approx 32,64 \right.$ cm.

Tổng quãng đường $L$ là: $L = 266 + 32,64 + 70 \approx 369\text{~cm}$

Đáp án cần điền là: 369

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.