Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc TN THPT và ĐGNL HCM - Ngày 07-08/02/2026
 ↪ TN THPT - Trạm 3 ↪ ĐGNL HCM
Giỏ hàng của tôi
Trang chủ
Toán11

Anh Việt có một tấm nhôm hình tam giác đều $ABC$ với cạnh bằng $6\left( {dm}

Câu hỏi số 856612:
Vận dụng

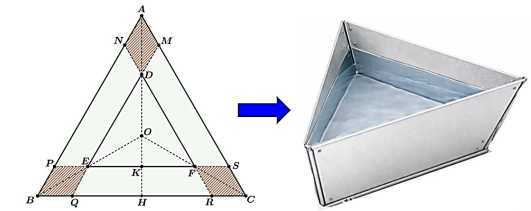
Anh Việt có một tấm nhôm hình tam giác đều $ABC$ với cạnh bằng $6\left( {dm} \right)$. Bên trong tấm nhôm này, anh vẽ thêm tam giác đều $DEF$ sao cho hai tam giác có cùng trọng tâm, đồng thời các cạnh tương ứng song song nhau. Anh Việt muốn làm một chậu đựng nước dạng hình chóp cụt tam giác đều với đáy nhỏ là $DEF$ và đáy lớn để hở.

Anh cắt bỏ ba hình bình hành ở ba góc của tam giác $ABC$ là $AMDN,\,\, BPEQ,\,\, CSFR$ (như hình). Kẻ đường cao $AH$ và gọi $O$ là trọng tâm tam giác $ABC$. Đặt $x = DN = DM\,\,\left( {0 < x < 2} \right)$

Đúng Sai
a) $NP = QR = SM = 6 - 2x\,\,\left( {dm} \right)$
b) $AH = 3\sqrt{3}\,\,\left( {dm} \right),\,\, OA = 2\sqrt{3}\,\,\left( {dm} \right)$
c) $AD = x\sqrt{3}\,\,\left( {dm} \right),\,\, DE = 6 - 3x\,\,\left( {dm} \right)$
d) Sau khi gập hình và dùng keo dán kín các đoạn gập vào nhau gồm $DM$ với $DN,\,\, EP$ với $EQ,\,\, FS$ với $FR$, sức chứa tối đa của chậu xấp xỉ $4,54\,\,(l)$

Đáp án đúng là: Đ; Đ; Đ; Đ

Quảng cáo

Xem lời giải
Câu hỏi:856612
Phương pháp giải

Chứng minh các phần cắt đi là hình thoi để tính cạnh đáy lớn và cạnh đáy nhỏ của hình chóp cụt theo biến $x$.

Tính chiều cao h của hình chóp cụt dựa vào độ dài cạnh bên ($x$) và hiệu bán kính đường tròn ngoại tiếp hai đáy.

Thiết lập công thức thể tích hình chóp cụt $V(x) = \dfrac{h}{3}(S_1 + S_2 + \sqrt{S_1 S_2})$.

Sử dụng đạo hàm để tìm giá trị lớn nhất của hàm số $V(x)$ trên khoảng $(0; 2)$.

Giải chi tiết

a) Đúng: Ta chứng minh được các hình bình hành $AMDN,\,\, BPEQ,\,\, CSFR$ là hình thoi

Khi đó $AN = BP = x$ nên $NP = AB - AN - BP = 6 - x - x = 6 - 2x$

b) Đúng: $AH = \dfrac{AB\sqrt{3}}{2} = \dfrac{6\sqrt{3}}{2} = 3\sqrt{3}\,\,\left( {dm} \right),\,\, OA = \dfrac{2}{3}AH = \dfrac{2}{3}.3\sqrt{3} = 2\sqrt{3}\,\,\left( {dm} \right)$

c) Đúng: Theo định lí cosin ta có:

$AD = \sqrt{AM^{2} + MD^{2} - 2AM.MD.\cos 120{^\circ}} = x\sqrt{3}$

$\Delta DEF \backsim \Delta ABC$ theo tỉ số $k$ nên $\dfrac{OE}{OB} = k$

Ta có: $OB = 2\sqrt{3},\,\, OE = OB - EB = 2\sqrt{3} - x\sqrt{3} = \left( {2 - x} \right)\sqrt{3}$

Do đó $k = \dfrac{\left( {2 - x} \right)\sqrt{3}}{2\sqrt{3}} = \dfrac{2 - x}{2}$

Khi đó $DE = \dfrac{2 - x}{2}.6 = 6 - 3x$

d) Đúng: Chậu nước có dạng hình chóp cụt tam giác đều với:

Cạnh đáy lớn $a_1=6-2x$; cạnh đáy nhỏ $a_2=6-3x$;

Cạnh bên $L=x$ (là các đoạn gấp lên như $DM, DN, EP, \dots$)

Gọi $R_1$ và $R_2$ lần lượt là bán kính đường tròn ngoại tiếp đáy lớn và đáy nhỏ.

$R_1 = \dfrac{a_1}{\sqrt{3}} = \dfrac{6-2x}{\sqrt{3}}$; $R_2 = \dfrac{a_2}{\sqrt{3}} = \dfrac{6-3x}{\sqrt{3}}$

Suy ra $h = \sqrt{L^2 - (R_1 - R_2)^2}$

              $= \sqrt{x^2 - \left( \dfrac{(6-2x) - (6-3x)}{\sqrt{3}} \right)^2} = \sqrt{x^2 - \left( \dfrac{x}{\sqrt{3}} \right)^2}= \dfrac{x\sqrt{6}}{3}$

Diện tích hai đáy là $S_1 = \dfrac{a_1^2\sqrt{3}}{4}$ và $S_2 = \dfrac{a_2^2\sqrt{3}}{4}$.

Thể tích hình chóp cụt: $V = \dfrac{h}{3}(S_1 + S_2 + \sqrt{S_1S_2})$

$V(x) = \dfrac{1}{3} \cdot \dfrac{x\sqrt{6}}{3} \cdot \dfrac{\sqrt{3}}{4} \left[ (6-2x)^2 + (6-3x)^2 + (6-2x)(6-3x) \right]$

       $= \dfrac{\sqrt{2}}{12} (19x^3 - 90x^2 + 108x)$

Xét hàm số $f(x) = 19x^3 - 90x^2 + 108x$

Có $f'(x) = 57x^2 - 180x + 108=0 \Leftrightarrow x = \dfrac{30 - 6\sqrt{6}}{19} \in (0;2)$.

Vậy $V_{max}= \dfrac{\sqrt{2}}{12} \left[ 19.\left(\dfrac{30 - 6\sqrt{6}}{19}\right)^3 - 90.\left(\dfrac{30 - 6\sqrt{6}}{19}\right)^2 + 108.\left(\dfrac{30 - 6\sqrt{6}}{19}\right) \right] \approx 4,54$ lít.

Đáp án cần chọn là: Đ; Đ; Đ; Đ

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn