Một đèn lồng đón năm mới được thiết kế theo hình bát diện đều (ta

Câu hỏi số 856617:

Vận dụng

Một đèn lồng đón năm mới được thiết kế theo hình bát diện đều (ta có thể hình dung hình bát diện đều là hai hình chóp tứ giác đều có tất cả cạnh bằng nhau S.ABCD và T.ABCD sử dụng chung một mặt đáy). Nghệ nhân đã thiết kế sẵn 12 tấm bìa cứng là các tam giác bằng nhau gồm 3 màu xanh, đỏ, vàng; các tấm bìa cùng màu được đánh số từ 1 tới 4. Mỗi tấm bìa khi dán vào đèn lồng sẽ vừa kín một trong tám mặt bên của nó. Gọi N là số cách mà nghệ nhân có thể chọn 8 tấm bìa dán lên 8 mặt bên của đèn lồng sao cho hai tấm bìa có chung một cạnh thì khác màu, hai tấm bìa có chung đúng một đỉnh thì khác số. Giá trị $\dfrac{N}{8} + 16$ bằng bao nhiêu?

Trả lời:

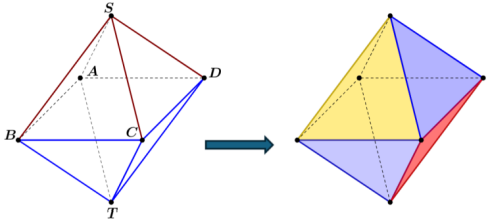
Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:856617

Phương pháp giải

Phân nhóm mặt: Chia 8 mặt của bát diện thành 2 nhóm độc lập $U$ và $V$ (mỗi nhóm gồm 4 mặt không có cạnh chung).

Đếm số cách gán số ($T_1$): Dựa trên ràng buộc "chung đúng một đỉnh thì khác số". Trong mỗi nhóm 4 mặt, hai mặt bất kỳ luôn chung ít nhất một đỉnh, nên mỗi nhóm phải dùng đủ bộ 4 số $\{1, 2, 3, 4\}$.

Đếm số cách tô màu ($T_2$): Dựa trên ràng buộc "chung cạnh thì khác màu". Vì các cạnh chỉ nối một mặt nhóm $U$ với một mặt nhóm $V$, ta xét các trường hợp phối màu của nhóm $U$ để suy ra cách tô màu nhóm $V$.

Tính tổng số cách $N = T_1.T_2$.

Giải chi tiết

Chia 8 mặt của bát diện thành 2 nhóm:

$U = \left\{ {\left( {SAB} \right),\,\,\left( {SCD} \right),\,\,\left( {TBC} \right),\,\,\left( {TAD} \right)} \right\},$

$V = \left\{ {\left( {SBC} \right),\left( {SAD} \right),\left( {TCD} \right),\left( {TAB} \right)} \right\}$

* Đếm số cách gán số cho 8 mặt:

Vì 2 mặt bất kì trong $U$ đều có chung 1 đỉnh nên nó phải khác số

Do đó 4 mặt trong $U$ phải mang đủ 4 số, mỗi mặt mang 1 số trong $\left\{ {1;2;3;4} \right\}$

Tương tự ta thấy 4 mặt trong $V$ cũng phải mang đủ 4 số

Vì 2 mặt bất kì trong $U$ đều khác số nên ta có $4!$ cách gán số cho các mặt nhóm $U$

Tương tự cũng có $4!$ cách gán số cho các mặt nhóm $V$

Vậy ta có $T_{1} = \left( {4!} \right)^{2} = 576$ (cách)

* Đếm số cách tô màu cho 8 mặt:

Trường hợp 1: Các mặt nhóm $U$ cùng sử dụng 1 màu

Giả sử 4 mặt của $U$ cùng dùng màu đỏ. Vì mỗi mặt của $V$ đều kề với đúng 3 mặt của $U$ nên khi 4 mặt của $U$ màu đỏ thì mỗi mặt của $V$ chỉ còn 2 cách chọn màu (xanh hoặc vàng)

Như vậy trường hợp 1 có $3.2^{4} = 48$ cách

Trường hợp 2: Các mặt nhóm $U$ sử dụng đúng 2 màu

Trường hợp 2a: Có 3 mặt cùng màu và 1 mặt khác màu với 3 mặt kia

Có $C_{3}^{2}$ cách chọn màu cho $U$

Có $C_{4}^{3}$ cách chọn 3 trong 4 mặt của $U$ để tô màu giống nhau

Giả sử các mặt của $U$ là Đ-X-X-X, khi đó 3 mặt còn lại trong $V$ chỉ còn 1 cách tô màu vàng, chỉ có duy nhất mặt đối xứng với mặt Đ của $U$ có thể tô 2 màu đỏ hoặc vàng. Nhưng nó không thể tô vàng vì nếu tô vàng sẽ trùng với trường hợp 1 (cả 4 mặt màu vàng)

Như vậy có $2!.C_{3}^{2}.C_{4}^{3} = 24$ (cách)

Trường hợp 2b: Có 2 mặt cùng màu và 2 mặt khác màu với 2 mặt kia

Có $C_{3}^{2}$ cách chọn màu cho $U$

Có $C_{4}^{2}$ cách chọn 2 trong 4 mặt của $U$ để tô màu giống nhau

Giả sử các mặt của $U$ là Đ-Đ-X-X, khi đó mỗi mặt của $V$ đều kề với 2 mặt (Đ và X) của $U$ nên chúng chỉ có thể tô màu vàng

Như vậy có $2!.1.C_{3}^{2}.C_{4}^{3} = 36$ cách

Trường hợp 3: Các mặt nhóm $U$ sử dụng đủ 3 màu

Ta thấy trường hợp 3 này không xảy ra

Vì giả sử các mặt của $U$ là Đ-X-V-Đ. Khi đó ta gọi mặt $v_{i}$ là mặt đối xứng với mặt Đ của $U$. Khi đó mặt $v_{i}$ đang kề với 3 mặt của $U$ đã có đủ 3 màu nên không thể tô màu cho $v_{i}$

Như vậy $T_{2} = 48 + 24 + 36 = 108$ (cách)

Vậy số cách nghệ nhân có thể thực hiện là $N = T_{1}.T_{2} = 62208$ cách

Khi đó $\dfrac{N}{8} + 6 = 7792$

Đáp án cần điền là: 7792

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.