Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn toán

 Một chậu nước có dạng một khối tròn xoay với thiết diện qua trục của chậu

Câu hỏi số 860274:
Vận dụng

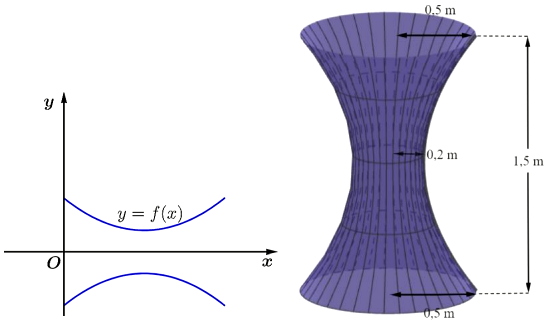
 Một chậu nước có dạng một khối tròn xoay với thiết diện qua trục của chậu (mặt cắt đi qua hai tâm của hai đường tròn đáy) là hai đường parabol đối xứng nhau qua trục đó. Biết hai đường tròn đáy chậu cùng có bán kính 0,5m; thiết diện nhỏ nhất vuông góc với trục của chậu có bán kính 0,2m; chiều cao của chậu nước bằng 1,5m. Người ta bơm nước vào chậu với tốc độ 5 lít/phút.

Xét hệ trục tọa độ Oxy với gốc O trùng với tâm đường tròn đáy của chậu nước, tia Ox chứa trục của chậu nước (đơn vị trên mỗi trục là mét). Mặt cắt qua trục của chậu nước cho ta hai nhánh parabol như hình vẽ, gọi $y = f(x)$ là parabol nằm trên trục hoành.

Đúng Sai
a) $f(x) = \dfrac{8}{15}x^{2} - \dfrac{4}{5}x + \dfrac{1}{2}$.
b) Sức chứa tối đa của chậu nước bằng $0,5~\text{m}^{3}$ (làm tròn đến hàng phần chục của mét khối).
c) Sau 1,5 giờ bơm nước (làm tròn đến hàng phần chục của giờ) thì chậu đầy nước.
d) Nếu bơm từ đầu như thế thì đến phút thứ 20, tốc độ dâng lên của nước bằng $0,01\text{m}/$ phút.

Đáp án đúng là: Đ; Đ; Đ; S

Quảng cáo

Xem lời giải
Câu hỏi:860274
Phương pháp giải

Áp dụng công thức tính thể tích khối tròn xoay quanh trục Ox.

Giải chi tiết

a) Đúng: Phương trình đường Parabol có dạng $f(x) = ax^{2} + bx + c(a \neq 0)$.

Parabol có tọa độ đỉnh là $(0,75;0,2)$ và đi qua hai điểm có tọa độ là $(0;0,5)$ và $(1,5;0,5)$.

Suy ra $\left\{ \begin{matrix} {a \cdot 0^{2} + b \cdot 0 + c = 0,5} \\ {a \cdot 1,5^{2} + b \cdot 1,5 + c = 0,5} \\ {a \cdot 0,75^{2} + b \cdot 0,75 + c = 0,2} \end{matrix} \right.$ $\left. \Rightarrow\left\{ \begin{array}{l} {a = \dfrac{8}{15}} \\ {b = \dfrac{- 4}{5}} \\ {c = \dfrac{1}{2}} \end{array} \right. \right.$

$\left. \Rightarrow f(x) = \dfrac{8}{15}x^{2} - \dfrac{4}{5}x + \dfrac{1}{2} \right.$

b) Đúng: Thể tích của chậu nước là:

$V = \pi{\int_{0}^{1,5}f^{2}}(x)dx = \pi{\int_{0}^{1,5}\left\lbrack {\dfrac{8}{12}x^{2} - \dfrac{4}{5}x + \dfrac{1}{2}} \right\rbrack^{2}}dx \approx 0,5\left( m^{3} \right)$.

Vậy sức chứa tối đa của chậu nước xấp xỉ $0,5~\text{m}^{3}$.

c) Đúng: Thời gian để bơm đầy bể là : $\dfrac{V.10^{3}}{5}.\dfrac{1}{60} \approx 1,5$ (giờ)

d) Sai: Sau 20 phút thì khối lượng nước bơm được là: $V_{1} = 5.20 = 100$ (lít) $= 0,1\left( {~\text{m}^{3}} \right)$.

Khi $t = 20$ phút thì $x = h$, ta có:

$V = \pi{\int_{0}^{h}f^{2}}(x)dx = \pi{\int_{0}^{h}\left\lbrack {\dfrac{8}{12}x^{2} - \dfrac{4}{5}x + \dfrac{1}{2}} \right\rbrack^{2}}dx$

$= \pi\left( {\dfrac{64}{1125}h^{5} - \dfrac{16}{75}h^{4} + \dfrac{88}{225}h^{3} - \dfrac{2}{5}h^{2} + \dfrac{1}{4}h} \right)$

Suy ra ta có phương trình $\pi\left( {\dfrac{64}{1125}h^{5} - \dfrac{16}{75}h^{4} + \dfrac{88}{225}h^{3} - \dfrac{2}{5}h^{2} + \dfrac{1}{4}h} \right) = 0,1$

$\left. \Rightarrow h \approx 0,164 = A \right.$

Tốc độ dâng lên của nước là: $\dfrac{A}{20} \approx 0,0082 \neq 0,01(~\text{m}/$phút) (Đề bài không yêu cầu làm tròn).

Đáp án cần chọn là: Đ; Đ; Đ; S

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn