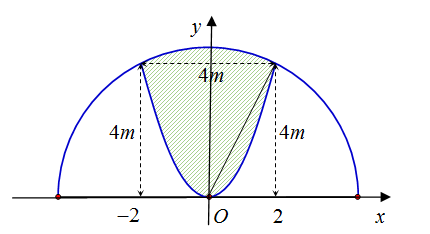
Một khuôn viên dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của

Câu hỏi số 861325:

Vận dụng

Một khuôn viên dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu) và cách nhau một khoảng bằng $4(m)$. Phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ, chi phí để trồng hoa và cỏ Nhật Bản tương ứng là $150.000$ đồng/m² và $100.000$ đồng/m². Hỏi cần bao nhiêu tiền (đơn vị: đồng) để trồng hoa và trồng cỏ Nhật Bản trong khuôn viên đó? (Số tiền được làm tròn đến hàng nghìn)

Đáp án:

Đáp án đúng là: 3739

Quảng cáo

Xem lời giải

Câu hỏi:861325

Phương pháp giải

Gắn hệ trục toạ độ Oxy. Xác định phương trình parabol và đường tròn

Tính diện tích bằng tích phân

Công thức diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f(x),y = g(x)$ liên tục trên đoạn $\left\lbrack {a;b} \right\rbrack$ và hai đường thẳng $x = a,x = b(a < b)$ là $S = \int_{a}^{b}\left| {f(x) - g(x)} \right|dx$

Giải chi tiết

$C:\Users\admin\Desktop\113.PNG$

Chọn hệ trục $Oxy$ như hình vẽ, ta có bán kính của đường tròn là $R = \sqrt{4^{2} + 2^{2}} = 2\sqrt{5}$.

Phương trình của nửa đường tròn $(C)$ là: $\left. x^{2} + y^{2} = 20\,,\, y \geq 0\Rightarrow y = \sqrt{20 - x^{2}} \right.$.

Parabol $(P)$ có đỉnh $O\left( {0\,;\, 0} \right)$ và đi qua điểm $\left( {2\,;\, 4} \right)$nên có phương trình: $y = x^{2}$.

Diện tích phần tô màu là: $S_{1} = {\int\limits_{- 2}^{2}{\left\lbrack {\sqrt{20 - x^{2}} - x^{2}} \right\rbrack\text{d}x}} \approx 11,94$$\left( m^{2} \right)$.

Diện tích phần không tô màu là: $S_{2} = \dfrac{1}{2}.\pi.\left( {2\sqrt{5}} \right)^{2} - S_{1} \approx 10\pi - 11,94$$\left( m^{2} \right)$.

Số tiền để trồng hoa và trồng cỏ Nhật Bản trong khuôn viên đó là:

$150000.11,94 + 100000.\left( {10\pi - 11,94} \right) \approx 3.738.593$.

Đáp án cần điền là: 3739

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.