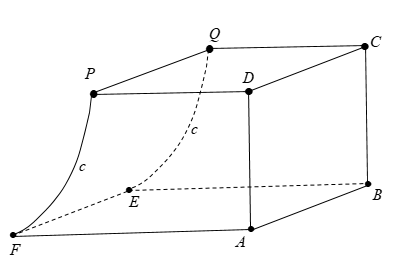
Một chi tiết máy được thiết kế như hình vẽ bên. Các tứ giác $ABCD,CDPQ$ là các hình vuông
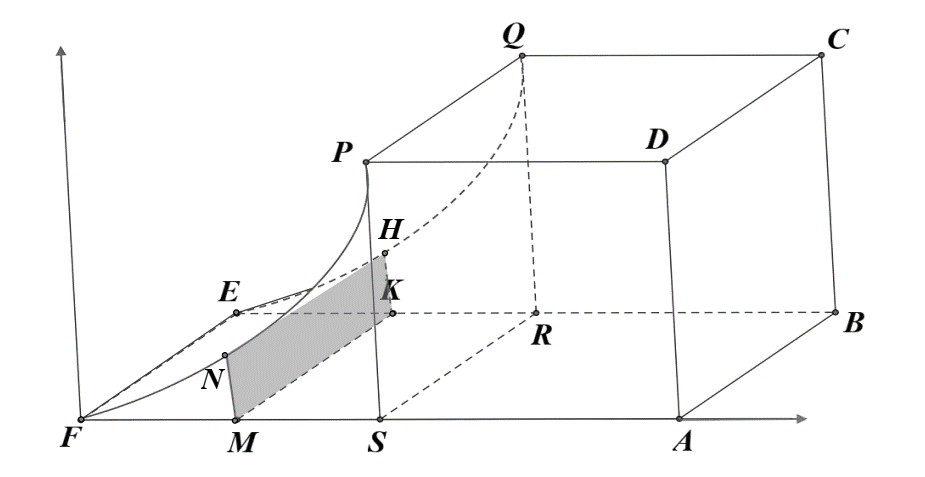
Một chi tiết máy được thiết kế như hình vẽ bên. Các tứ giác $ABCD,CDPQ$ là các hình vuông cạnh $2,5\, cm$. Tứ giác $ABEF$ là hình chữ nhật có $BE = 3,5\, cm$. Mặt bên$PQEF$được mài nhẵn theo đường parabol $(P)$ có đỉnh parabol nằm trên cạnh $EF$. Thể tích của chi tiết máy bằng bao nhiêu $cm^{3}$
Quảng cáo
Đặt hệ trục $Oxyz$ sao cho $O$ trùng với$F$, $Ox$ trùng với$FA$, $Oy$ trùng với tia $Fy$ song song với $AD$.
Viết phương trình Parabol $(P)$có dạng$y = ax^{2}$ từ đó tính diện tích thiết diện mặt cắt
Khi đó thể tích bằng tích phân $V = {\int\limits_{a}^{b}{S(x)}}dx$
Gọi hình chiếu của $P,\, Q$ trên $AF$ và $BE$ là $R$ và$S$.
Vật thể được chia thành hình lập phương $ABCD.PQRS$ có cạnh $2,5\, cm$, thể tích $V_{1} = \dfrac{125}{8}\, cm^{3}$ và phần còn lại có thể tích $V_{2}$.
Khi đó thể tích vật thể $V = V_{1} + V_{2} = \dfrac{125}{8} + V_{2}$.
Đặt hệ trục $Oxyz$ sao cho $O$ trùng với$F$, $Ox$ trùng với$FA$, $Oy$ trùng với tia $Fy$ song song với $AD$.
Khi đó Parabol $(P)$có phương trình dạng$y = ax^{2}$, đi qua điểm $P\left( {1;\dfrac{5}{2}} \right)$ do đó $\left. a = \dfrac{5}{2}\Rightarrow y = \dfrac{5}{2}x^{2} \right.$.
Cắt vật thể bởi mặt phẳng vuông góc với $Ox$ và đi qua điểm $M\left( {x;0;0} \right),\, 0 \leq x \leq 1$ ta được thiết diện là hình chữ nhật $MNHK$ có cạnh là $MN = \dfrac{5}{2}x^{2}$ và $MK = \dfrac{5}{2}$do đó diện tích $S(x) = \dfrac{25}{4}x^{2}$
Áp dụng công thức thể tích vật thể ta có $V_{2} = {\int\limits_{0}^{1}{\dfrac{25}{4}x^{2}dx}} = \dfrac{25}{12}$
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
