Một xưởng mộc dự định sản xuất hai loại hàng hóa là bàn và ghế. Để sản xuất một cái

Câu hỏi số 861330:

Vận dụng

Một xưởng mộc dự định sản xuất hai loại hàng hóa là bàn và ghế. Để sản xuất một cái bàn cần 6 giờ công đoạn cắt và 2 giờ công đoạn hoàn thiện. Để sản xuất một cái ghế cần 3 giờ công đoạn cắt và 3 giờ công đoạn hoàn thiện. Biết rằng bộ phận cắt làm việc tối đa 120 giờ/tháng và bộ phận hoàn thiện làm việc tối đa 60 giờ/tháng. Lợi nhuận thu về của mỗi cái bàn là 600 nghìn đồng và mỗi cái ghế là 400 nghìn đồng. Hỏi xưởng nên sản xuất bao nhiêu cái bàn và ghế để thu được lợi nhuận cao nhất?

Quảng cáo

Xem lời giải

Câu hỏi:861330

Phương pháp giải

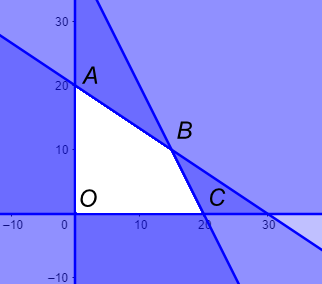
Đưa về bài toán tối ưu hệ bất phương trình bậc nhất hai ẩn, biểu diễn miền nghiệm và đạt cực đại tại một trong các đỉnh của đa giác miền nghiệm

Giải chi tiết

Gọi $x,~y$ lần lượt là số lượng bàn và ghế cần sản xuất $\left( {x~ \geq ~0,~y~ \geq ~0,~x,~y~ \in ~N} \right).$

Số tiền lãi thu được trong một tháng là: $F\left( {x;~y} \right)~ = ~600x~ + ~400y$ (nghìn đồng)

Theo đề bài, thời gian làm việc của bộ phận cắt không quá 120 giờ và bộ phận hoàn thiện không quá 60 giờ, ta có các bất phương trình: $6x~ + ~3y~ \leq ~120$ hay $2x~ + ~y~ \leq ~40$ và $2x~ + ~3y~ \leq ~60$

Kết hợp với điều kiện số lượng không âm, ta có hệ bất phương trình mô tả các điều kiện ràng buộc: $\left\{ \begin{matrix} {2x~ + ~y~ \leq ~40~(1)~} \\ {~2x~ + ~3y~ \leq ~60~(2)} \\ {x~ \geq ~0} \\ {y~ \geq ~0} \end{matrix} \right.$

Miền nghiệm của hệ bất phương trình là tứ giác $OABC$ được giới hạn bởi các đường thẳng, với các đỉnh: $O\left( {0;~0} \right)$; $A\left( {0;~20} \right)$; $C\left( {20;~0} \right)$; $B\left( {15;~10} \right).$

Ta tính giá trị của hàm mục tiêu $F\left( {x;~y} \right)$ tại các đỉnh của miền nghiệm:

Tại $O\left( {0;~0} \right)$: $F~ = ~0$

Tại $A\left( {0;~20} \right)$: $F~ = ~600.0~ + ~400.20~ = ~8000$(nghìn đồng)

Tại $B\left( {15;~10} \right)$: $F~ = ~600.15~ + ~400.10~ = ~~13000$ (nghìn đồng)

Tại $C\left( {20;~0} \right)$: $F~ = ~600.20~ + ~400.0~ = ~12000$ (nghìn đồng)

So sánh các kết quả, ta thấy giá trị lớn nhất là 13000 (nghìn đồng).

Giá trị này đạt được khi $x~ = ~15$ và $y~ = ~10$.

Vậy để thu được lợi nhuận cao nhất (13 triệu đồng), xưởng nên sản xuất 15 cái bàn và 10 cái ghế.

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.