Góc với đường tròn
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài 71:
Một đường tròn (O) đi qua đỉnh A của góc xAy cắt Ax, Ay lần lượt tại các điểm B, C sao cho AC > AB. Đường trung trực của BC cắt cung BAC tại điểm D. Lấy các điểm M, N tương ứng trên các tia Bx, Cy sao cho BM = CN.
Câu hỏi số 1:
So sánh ![]() với
với ![]() .Suy ra hai tam giác DBM và DCN bằng nhau.
.Suy ra hai tam giác DBM và DCN bằng nhau.
Câu hỏi số 2:
Chứng minh rằng bốn điểm D, A, M, N nằm trên một đường tròn.
Câu hỏi số 3:
Bốn điểm B, C, M, N có nằm trên một đường tròn không? Tại sao?
Bài 72:
Từ một điểm S nằm ngoài một đường tròn (O), người ta kẻ tới (O) một tiếp tuyến SA và một cát tuyến SBC sao cho ![]() < 90°. Tia phân giác của góc BAC cắt dây BC tại điểm D và cắt đường tròn (O) tại điểm thứ hai E. Các tiếp tuyến của (O) tại C, E cắt nhau tại điểm N. Gọi Q, P theo thứ tự là giao điểm của các cặp đường thẳng AB và CE; AE và CN.
< 90°. Tia phân giác của góc BAC cắt dây BC tại điểm D và cắt đường tròn (O) tại điểm thứ hai E. Các tiếp tuyến của (O) tại C, E cắt nhau tại điểm N. Gọi Q, P theo thứ tự là giao điểm của các cặp đường thẳng AB và CE; AE và CN.
Câu hỏi số 1:
Chứng minh SA = SD
Câu hỏi số 2:
Chứng minh EN song song với BC
Câu hỏi số 3:
So sánh hai tam giác QCB và PCE.
Câu hỏi số 4:
Chứng minh hệ thức : 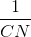 =
= 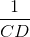 +
+ 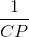
Bài 73:
Cho tam giác ABC cân (AB = AC) có ba đỉnh nằm trên đường tròn (O) và một điểm M bất kì trên cung nhỏ AC. Tia Bx vuông góc với AM cắt tia CM tại D.
Câu hỏi số 1:
Chứng minh 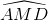 =
= 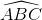
Câu hỏi số 2:
Chứng minh tam giác BMD cân
Câu hỏi số 3:
Chứng minh rằng khi M di động thì D chạy trên một đường tròn cố định.
Câu hỏi số 4:
Xác định vị trí của M để tứ giác ABMD là hình thoi. Tính AM ở vị trí đó biết
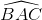 = α và bán kính đường tròn O là R.
= α và bán kính đường tròn O là R.
Bài 74:
Cho hai đường tròn (O1;R1) và (O2;R2) (R1<R2) tiếp xúc ngoài với nhau tại A .Kẻ các đường kính AO1Bvà AO2C.Gọi DElà tiếp tuyến chung ngoài của hai đường tròn (D∈(O1),E∈(O2)).Gọi M là giao điểm của BD và CE.
Câu hỏi số 1:
Chứng minh MA là tiếp tuyến chung cua hai đường tròn.
Câu hỏi số 2:
Gọi giao điểm của DE với AB là J .Tính JA theo R1 theo R2
Câu hỏi số 3:
Gọi (O;R)tiếp xuc với DE đồng thời tiếp xúc ngoài với (O1;R1) và (O2;R2). Chứng minh rằng :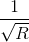 =
=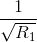 +
+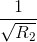
Bài 75:
Cho đường tròn (O; R) với ba dây liên tiếp AB, BC, CD bằng nhau và cùng nhỏ hơn R. Các đường thẳng AB, CD cắt nhau tại điểm I, các tiếp tuyến của đường tròn tại B, D cắt nhau tại điểm K.
Câu hỏi số 1:
So sánh các góc BIC và BKD.
Câu hỏi số 2:
Chứng minh rằng BC nằm trên tia phân giác của góc KBD.
Câu hỏi số 3:
Chứng minh rằng các cặp hai tam giác IBC và KBD ; CBD và IBK đồng dạng.
Câu hỏi số 4:
Chứng minh rằng IK song song với BC.
Bài 76:
Cho đường tròn (O). Đường kính AB chia đường tròn thành hai nửa đường tròn và các điểm C, D nằm trên hai nửa đường tròn ấy. Gọi M, N theo thứ tự là các điểm chính giữa của các cung AC, AD, các giao điểm của MN với AC, AD tương ứng là E, F.
Câu hỏi số 1:
Chứng minh tam giác AEF cân.
Câu hỏi số 2:
Gọi giao điểm của của CN và DM là P. Xác định các giao điểm của hai đường tròn (M; MA) và (N; NA).
Câu hỏi số 3:
Giả sử các cung AC, AD không bằng nhau. Các đường thẳng MN, CD cắt nhau tại điểm H và cắt tiếp tuyến tại A của đường tròn (O) theo thứ tự tại I, K. Tam giác HIK là tam giác gì ?
Câu hỏi số 77:
Hai dây cung AB và CD của đường tròn (O) cắt nhau tại E. Tính góc BEC nếu sđ cung AC = 42° , sđ cung BD = 128°
Câu hỏi số 78:
Từ một điểm ở ngoài đường tròn vẽ hai cát tuyến tạo với nhau một góc 45°. Cung lớn của đường tròn này tạo bởi hai cạnh của góc này bằng 120°. Tính cung nhỏ.
Câu hỏi số 79:
Điểm B1, C1 lần lượt là trung điểm của cung AB, AC (h.2c). Gọi M, N lần lượt là giao điểm của B1C1 với AB, AC. Chứng minh rằng AM = AN.

Bài 80:
Cho hai đường tròn đồng tâm và một điểm M cố định trên đường tròn nhỏ. Qua M kẻ hai đường thẳng vuông góc với nhau, một đường cắt đường tròn nhỏ tại A khác M, đường kia cắt đường tròn lớn ở B và C. Khi hai đường thẳng này quay quanh M mà vẫn vuông góc với nhau. Chứng minh:
Câu hỏi số 1:
Tổng MA2 + MB2 + MC2 không đổi.
Câu hỏi số 2:
Trọng tâm tam giác ABC là điểm cố định.
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com









